آموزش
معاون آموزشی دانشکدهی ریاضی، دکتر رضا مختاری هستند. دو کارشناس آموزشی دانشکده، آقایان مهدی حجارزاده و منوچهر میرزائی در اجرای امور آموزشی با دانشکده همکاری میکنند. در زیر مشخصات دقیق این افراد قرار گرفته است:
دکتر رضا مختاری، دانشیار دانشکدهی ریاضی و معاون آموزشی، شمارهی تلفن اتاق: ۰۳۱۳۳۹۱۳۶۱۴
آقای مهدی حجارزاده، کارشناس آموزشی، شمارهی تلفن: ۰۳۱۳۳۹۱۳۶۱۸
آقای منوچهر میرزائی، کارشناس آموزشی، شمارهی تلفن: ۰۳۱۳۳۹۱۳۶۲۹
به طور کلی آموزش دانشکده، مسئول امور ثبتنام، بررسی روند تحصیلی دانشجویان، تغییر رشته، انتقال و فارغالتحصیلی است. اطلاعیهها و آییننامههای مربوط به هر کدام از موارد ذکر شده، در بخش «اطلاعیهها و آییننامهها» موجود هستند.
اساتید راهنمای دانشجویان ورودی جدید، به ترتیب دکتر خانی و دکتر سلطانی برای گروه ریاضی و دکتر گلی و دکتر سلامت برای گروه آمار هستند. به زودی صفحهای در بخش آموزش برای آنها احداث خواهد شد. این اساتید، نودانشجویان را در طول تحصیلشان راهنمائی خواهند کرد.
برای اطلاع، وظایف آموزش دانشکده، به صورت دقیقتر در زیر بیان شده است:
- امور آموزشی: ثبت نام، ترمیم، ثبت نام مقدماتی، حذف اضطراری، امتحانات در طول هر ترم و نظارت بر حسن اجرای آن.
- اجرای مصوبات شورای برنامهریزی آموزشی دانشگاه.
- هماهنگی بین گروههای آموزشی و همکاری با اساتید راهنما و مدیران محترم گروهها از بدو پذیرش تا صدور صورتجلسه فارغالتحصیلی.
- بررسی روند تحصیلی دانشجویان از نظر مشروطی، سنوات و تعداد واحد اخذ شده.
- تنظیم صورتجلسه فارغالتحصیلی دانشجویان و اعلام فراغت از تحصیل به اداره کل آموزش.
- رسیدگی به امور دانشجویان متقاضی مهمان و انتقال.
- بررسی درخواست متقاضیان تغییر رشته.
- انجام امور مربوط به ارتقای مرتبه و پایه اساتید.
آمار ریاضی ۱
تعداد واحد/ساعت: ۴ واحد/ ۶۸ ساعت
پیش نیاز: احتمال ۲
حل تمرین: ۱۷ ساعت
از جدول: ۵
سر فصل درس و ریزمواد:
- یادآوری و بیان تعاریف پایه و اساسی: مروری بر نظریه توزیعها، خانواده توزیع نمایی، خانواده توزیعهای مکان، خانواده توزیعهای مقیاس و مکان-مقیاس.
- بسندگی و کامل بودن: نمونه تصادفى، آمارهها و افرازها، آماره بسنده، آماره بسنده مینیمال، آماره کامل.
- روشهای براوردیابی: مفهوم براورد و تعریف براوردگر و براورد، براورد گشتاوری، روش درستنمایی ماکسیمم،
ویژگیها و خواص برآورد، سازگاری.
- براورگرهای نااریب با کمترین واریانس: براوردگرهای نااریب، براوردگرهای نااریب با کمترین واریانس، روشهای دستیابی، کارایی.
- نامساوی کرامر-رائو و اطلاع فیشر.
- آمار بیز: تابع زیان، تابع مخاطره، توزیع پیشین و پسین ، پیشین مزدوج، براورد بیزی.
مراجع :
- Introduction to the theory of Statistics, By: A. M. Mood, F. A. Graybill and D. C. Boes
- مبانی آمار رياضى ، احمد پارسيان، ویرایش دوم، انتشارات دانشگاه صنعتی اصفهان، 1383.
- آمار رياضى ، جواد بهبوديان، انتشارات آستان قدس رضوی، 1380.
آمار ریاضی 2
تعداد واحد/ساعت: 4 واحد/ 68 ساعت
پیش نیاز: آمار ریاضی ۱
حل تمرین: ۱۷ ساعت
از جدول: ۵
سر فصل درس و ریزمواد:
- (یادآوری: ارتباط بین توزیع ها)
- روشهای یافتن براورد فاصله ای: کمیت محوری، روش عمومی، روش تابع توزیع، فاصله اطمینان با دمهای برابر، کوتاهترین فاصله اطمینان، فاصله اطمینان نااریب، فاصله اطمینان با اندازه بزرگ.
(تذکر: در مباحث فوق نحوه یافتن فاصله اطمینان برای پارامترهای زیر بیان شود:
میانگین، واریانس و نسبت یک جامعه، تفاضل میانگینهای دو جامعه مستقل و غیر مستقل، نسبت واریانس دو جامعه مستقل و چندکها).
- آزمون فرضهای ساده: تعاریف و مفاهیم اولیهشامل فرض آماری، آماره آزمون، خطاهای آزمون، تابع آزمون، تابع توان و آزمون آماری، مفهوم p-مقدار، آزمون پرتوان، آزمون تصادفی، آزمون نسبت درستنمایی،
مقایسه دو آزمون فوق.
- پرتوانترین آزمون یکنواخت: تعاریف و مفاهیم متناظر با فرضهای مرکب، خاصیت MLR، نحوه یافتن آزمون UMP در فرضهای یکطرفه.
- آزمون نسبت درستنمایی تعمیم یافته: آزمون نسبت درستنمایی، توزیع مجانبی آماره LRT، ارتباط آزمون فرض آماری و فاصله اطمینان.
- چند آزمون کاربردی: آزمون نیکویی برازش، آزمون هم توزیعی و استقلال ( آزمون کای- دو).
- آمار بیز: تابع زیان، تابع مخاطره، توزیع پیشین و پسین ، پیشین مزدوج، براورد بیزی.
مراجع :
- Introduction to the theory of Statistics, By: A. M. Mood, F. A. Graybill and D. C. Boes
- مبانی آمار رياضى ، احمد پارسيان، ویرایش دوم، انتشارات دانشگاه صنعتی اصفهان، 1383.
- آمار رياضى ، جواد بهبوديان، انتشارات آستان قدس رضوی، 1380.
آمار ناپارامتری
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیش نیاز: احتمال ۲، روش های آماری
حل تمرین: حداقل ۲۵ ساعت
از جدول: ۳
سرفصلدرسوريزمواد :
- آماره های ترتیبی و کاربرد آن در آمار ناپارامتری :(آماره های ترتیبی، آماره های ترتیبی توزیع یکنواخت و خواص آنها، کاربرد آماره های ترتیبی برای چندک ها، آزمون نشانه )
- آماره های رتبه ای : (مفهوم رتبه در یک متغیر تصادفی، آزمون جمعی-رتبه ای ویلکاکسون، آزمون من-ویتنی)
- آزمون ناپارامتری با نمونه ای از دوتایی ها : ( آزمون نشانه با نمونه ای از دوتایی، آزمون رتبه ای-نشانه ای از ویلکاکسون)
- فصل چهارم: همبستگی دو متغیر تصادفی : (ضریب همبستگی ساده، ضریب رتبه ای اسپرمن، ضریب همبستگی کندال
- دوها و کاربرد آنها در آمار ناپارامتری: ( تابع احتمال دوها، کاربرد دوها )
- آزمون های نیکویی برازش توزیع : ( آزمون کای دو، توزیع تجربی و آزمون های مربوط به آن )
مراجع:
- آمار ناپارامتری، جواد بهبودیان، مرکز نشر دانشگاه شیراز
- آمار ناپارامتری کاربردی، تالیف : کنوور، ترجمه : سید مقتدی هاشمی پرست، مرکز نشر دانشگاهی، تهران
آنالیز ریاضی ۱
ضرورت ارائهی درس
آنالیز ریاضی بررسی دقیق مفاهیم ارائه شده در دروس ریاضی عمومی بوده، مفاهیمی چون حد، پیوستگی، مشتق و انتگرال با عمق بیشتر و در چهارچوبی جامعتر بررسی میگردند. بسیاری از خاصیتهایی که در دروس ریاضی عمومی به راحتی و با تکیه بر شهود دانشجو پذیرفته میشوند، در اینجا اثبات میگردند. این امر علاوه بر افزایش مهارت دانشجو در درک مفاهیم مجرد و تحلیلی، به وی کمک میکند تا با روشهای مختلف اثبات آشنا گردد و به این ترتیب آماده ورود به دروس پیشرفتهتر شود. در درس آنالیز ریاضی 1، دانشجو مفاهیم حد، پیوستگی و مشتق را مورد مطالعه قرار میدهد. مفهوم حد، و در پی آن پیوستگی، در ساختاری کلیتر از مجموعه اعداد حقیقی، یعنی فضاهای متریک نیز قابل ارائه است. به همین دلیل، بعد از مرور خاصیتهای اصلی مجموعه اعداد حقیقی و بررسی دنبالهها و سریهای عددی، دانشجو با مفهوم فضای متریک و زیرمجموعههای خاص این فضا آشنا میشود. سپس مفاهیم حد و پیوستگی توابع بر روی این فضاها مورد مطالعه قرار گرفته، قضایای مهمی از حساب دیفرانسیل و انتگرال مانند قضیه مقادیر میانی و قضیه اکسترممهای مطلق بیان و ثابت میشوند.
شرح درس:
میدان اعداد حقیقی، کوچکترین کران بالا و بزرگترین کران پایین، خاصیت ارشمیدسی اعداد، چگالی اعداد گویا، چگالی اعداد اصم، دستگاه اعداد حقیقی گسترشیافته، دنبالههای عددی، همگرایی و واگرایی یک دنباله، دنبالههای یکنوا، حد بالا و پایین یک دنباله کراندار، دنباله کوشی، سری عددی، همگرایی و واگرایی یک سری، شرط کوشی برای همگرایی، آزمونهای همگرایی، همگرایی مطلق و مشروط، تجدید آرایش سری، فضای متریک، مجموعههای باز و بسته، مجموعههای فشرده، مجموعههای همبند، دنبالهها در یک فضای متریک، دنبالههای کوشی و فضاهای متریک تام، پیوستگی توابع، پیوستگی بر یک مجموعه، خاصیتهای توپولوژیک توابع پیوسته، پیوستگی و فشردگی، پیوستگی و همبندی، قضیه مقادیر میانی، پیوستگی یکنواخت، مشتق توابع حقیقی یک متغیره، قضیه مقادیر میانی برای مشتق.
آنالیز ریاضی ۲
ضرورت ارائهی درس
این درس از دو مبحث انتگرال ریمان-اشتیلیس و دنبالهها و سریهای تابعی تشکیل شده است. در بحث اول، انتگرال ریمان-اشتیلیس به عنوان یک تعمیم طبیعی انتگرال ریمان مطرح میشود. کاربرد اصلی این مفهوم در مباحثی شامل نظریه احتمال است. در این ساختار قضیه اساسی حساب دیفرانسیل و انتگرال با بیانی سازگار با آن بیان و اثبات میشود. در نهایت، شرط لبگ برای انتگرال پذیری ریمان دیدگاهی موثر در مورد توابعی که انتگرالپذیر ریمان هستند به دست میدهد. در بخش دوم دنبالههای و سریهای تابعی و انواع همگرایی آنها معرفی میشود. این بحث در ساختن توابعی با ویژگیهای مشخص بسیار مهم است. یکی از موارد استفاده مباحث اخیر در دروس معادلات دیفرانسیل عادی و پارهای است. سریهای توانی و فوریه به عنوان حالت خاصی از سریهای تابعی قابل بحث و تجزیه و تحلیل خواهند بود.
شرح درس
انتگرال ریمان-اشتیلیس نسبت به یک انتگرالگیر صعودی، انتگرالهای بالا و پایین، انتگرالپذیری نسبت به یک انتگرالگیر صعودی، شرط ریمان برای انتگرالپذیری، خواص انتگرال ریمان-اشتیلیس، توابع با تغییر کراندار، انتگرال ریمان-اشتیلیس نسبت به توابع با تغییر کراندار، انتگرالگیرهای مشتقپذیر، قضیه اساسی حساب دیفرانسیل و انتگرال، محک لبگ برای انتگرالپذیری ریمان، مجموعههای با اندازه صفر، دنبالههای تابعی، همگرایی نقطهوار و همگرایی یکنواخت، همگرایی یکنواخت و پیوستگی، مشتقپذیری و انتگرالپذیری، قضیه تقریب وایراشتراس، جبر توابع، قضیه اشتون-وایراشتراس، خانواده توابع همپیوسته، لم آرزلا-آسکولی، سریهای تابعی، آزمون M وایراشتراس، آزمون آبل برای همگرایی یکنواخت سری تابعی، سریهای توانی، شعاع همگرایی، سری فوریه.
آنالیز عددی ۱
ضرورت ارائهی درس
بسیاری از پدیدهها در علوم و مهندسی شامل حل مسایلی است که یافتن جواب آنها با روشهای متداول امکانپذیر نیست یا بسیار پیچیده است. این در صورتی است که جواب این مسایل وجود دارد و اهمیت زیادی برای کاربران دارد. مثالهای ملموس در این مورد یافتن ریشهها و محاسبه مقدار انتگرال معین توابع است که به وفور در حل مسایل کاربردی مشاهده میشوند. ضرورت یافتن راهکارهایی برای یافتن جواب این مسایل زمانی روشنتر میشود که با حجم بالایی از این مسایل به ویژه در ابعاد بالا روبرو هستیم. ایدههای اصلی برای حل اینگونه مسایل در این درس مورد بحث قرار میگیرند. از دیدگاه تاریخی اگرچه برخی از این ایدهها سابقهای بسیار طولانی دارند، معمولا همگام با ایجاد و توسعه کامپیوترها شکل گرفته و تکمیل شدهاند. در واقع برای حل یک مساله و پیادهسازی آن در کامپیوتر باید آن را گسسته سازی کرده و الگوریتمی برای یافتن جواب تقریبی آن مساله طراحی کرد. بنابراین میتوان آنالیز عددی را علم طراحی الگوریتم برای حل مسایل دانست بهطوری که جواب حاصل شده تقریب مناسبی از جواب تحلیلی مساله باشد. امروزه یک درس آنالیز عددی با اندکی تفاوت درسرفصلهایی که در ادامه میآید، در دوره کارشناسی تمام دانشگاههای معتبر دنیا ارایه شده و گذراندن یک درس اجباری در آنالیز عددی از ضروریات دوره کارشناسی محسوب میشود.
شرح درس:
منابع خطا، ساختار نمایش اعداد در کامپیوتر به صورت ممیز شناور و خصوصیات آن، انتشار خطا در محاسبه توابع، خوش وضعی مساله و پایداری یک الگوریتم، نحوه تقریب توابع با استفاده از بسط تیلور و برآورد خطای آن، وجود و یکتایی ریشه معادلات غیر خطی، روش دو بخشی، روش نابهجایی، روش تکرار نقطه ثابت، روش نیوتن- رافسون، روش وتری، همگرایی، تعبیر هندسی، برآورد خطا و معیارهای توقف این روشها، مرتبه همگرایی و ریشههای چندگانه، الگوریتم هورنر و روش نیوتن برای یافتن ریشههای چندجملهایها، برونیابی آیتکن، مساله درونیابی، وجود و یکتایی، درونیابی به روش لاگرانژ، خطای درونیابی، روش تفاضلات تقسیم شده نیوتن، روشهای تفاضلات پیشرو و پسرو برای نقاط با فاصله مساوی، مثال نقض رونگه، درونیابی بر اساس ریشههای چندجملهایهای چبیشف و برآورد خطای آن، اشاره به درونیابی هرمیت، اسپلاین خطی و اشاره به اسپلاینهای مکعبی، روشهای کمترین مربعات گسسته و پیوسته برای برازش چندجملهایها، روشهای ذوزنقهای، سیمپسون، نقطه میانی و یافتن فرمول خطای این روشها، درجه دقت یک قاعده انتگرالگیری، فرمولهای انتگرالگیری نیوتن کاتس، انتگرالگیری گاوسی، برونیابی ریچاردسون و قاعده انتگرالگیری رامبرگ، مشتقگیری عددی و بررسی مرتبه همگرایی و درجه دقت آنها با استفاده از بسط تیلور و درونیابی، ناپایداری در مشتقگیری عددی، پیاده سازی الگوریتمها با نرم افزار متلب.
احتمال ۱و ۲
زندگی روزمره ما بر اساس غیر قابل پیش بینی بودن آینده استوار است. بر این اساس، در مطالعه هر پدیده ای با پیشامدهایی روبرو می شویم که امکان رخ دادن یا رخ ندادن آنها وجود دارد. همانند پیروز شدن در یک مسابقه، موفق شدن در یک سرمایه گذاری و .... اینگونه پیشامدها را پیشامدهای تصادفی یا احتمالاتی می گوییم و به دنبال آن هستیم که با تکیه بر یکسری مفاهیم اصلی که در این درس معرفی می شوند، برای آنها معنی و مفهوم کمی و کیفی بیابیم. کمیتهای منتج از تصادفی بودن پدیده های مورد مطالعه، از توابعی که به آنها متغیرهای تصادفی گوییم، بدست می آیند که می توانند پیوسته، گسسته و یا تلفیقی از آن دو باشند.
سرفصل دروس:
احتمال 1:
اصول احتمال، فضای نمونه، پيشامدها، احتمال یک پيشامد، گزارههای احتمال و مدلهای احتمالی، پيوستگی تابع احتمال، احتمال شرطی و استقلال، قانون بيز و كاربردهای آن، متغيرهای تصادفی، تابع توزیع، متغيرهای تصادفی گسسته و توابع جرمی احتمال، اميد ریاضی و خواص آن، اميد ریاضی تابعی از متغير تصادفی گسسته، متغيرهای تصادفی گسسته خاص مانند برنولی، دوجمله ای، پوآسون، هندسی، دو جملهای منفی، فوق هندسی و زتا، متغير تصادفی پيوسته، توابع چگالی احتمال، اميد ریاضی و واریانس متغيرهای تصادفی پيوسته، متغيرهای تصادفی پيوسته خاص مانند یكنواخت، نرمال، نمایی، گاما، وایتل، كوشی و بتا.
احتمال 2:
متغيرهای تصادفی با توزیع توام، كوواریانس و ضریب همبستگی دو متغير تصادفی، متغيرهای تصادفی مستقل، توزیعهای شرطی، حالت گسسته و پيوسته، توزیع توام توابعی از متغيرهای تصادفی، اميد ریاضی شرطی و كاربردهای آن، نامساویهای احتمالی مانند ماركف و چبيشف، قانون ضعيف اعداد بزرگ، توابع مولد گشتاور و كاربردهای آن، قضيه حد مركزی.
مراجع:
- Ghahramani, S. (1996) Fundamentals of Probability, Printice Hall.
- Grimmett, G. R. and Stirzaker, D. R. (2001) Probability and Random Processes, Oxford University Press, 3rd ed.
- Grinstead, C.M. and Snell, J.L. (1977) Introduction to probability, 2nd revised ed., AMS.
- Ross, K.L. (2014) A first course in probability, 9th ed, Pearson Education Limited.
احتمال و کاربرد آن
ضرورت ارائهی درس:
احتمال یکی از دروس اصلی ریاضی است که در سالهای اخیر با توجه به وجود دادهها و به کارگیری آنها در تحقیقات و نیز کاربرد این علم پایهای در تحقیقات مهم ریاضی از اهمیت خاصی برخوردار است. دانشجویان ریاضی که مایل به انجام تحقیقات جدید و به روز هستند به آشنایی با این علم نیاز فراوان دارند.کارشناسان ریاضی هم که در نهادهای مختلف قصد برنامهریزی دارند برای پیشبینی آینده باید آشنایی وسیعی با علم احتمال داشته باشند. لذا وجود چنین درسی در دوره کارشناسی ریاضی جهت رسیدن به اهداف فوق کاملا ضروری است.
شرح درس:
اصول احتمال، فضای نمونه، پیشامدها، احتمال یک پیشامد، گزارههای احتمال و مدلهای احتمالی، پیوستگی تابع احتمال، احتمال شرطی و استقلال، قانون بیز و کاربردهای آن، متغیرهای تصادفی، تابع توزیع، متغیرهای تصادفی گسسته و تابع جرمی احتمال، امید ریاضی و خواص آن، امید ریاضی تابعی از متغیر تصادفی گسسته، متغیرهای تصادفی گسسته خاص مانند برنولی، دوجملهای، پوآسون، هندسی، دو جملهای منفی، فوق هندسی و زتا، متغیر تصادفی پیوسته، تابع چگالی احتمال، امید ریاضی و واریانس متغیرهای تصادفی پیوسته، متغیرهای تصادفی پیوسته خاص مانند یکنواخت، نرمال، نمایی، گاما، وایبل، کوشی و بتا، متغیرهای تصادفی با توزیع توام، کوواریانس و ضریب همبستگی دو متغیر تصادفی، متغیرهای تصادفی مستقل، توزیعهای شرطی، حالت گسسته و پیوسته، توزیع توام توابعی از متغیرهای تصادفی، امید ریاضی شرطی و کاربردهای آن، نامساویهای احتمالی مانند مارکف و چبیشف، قانون ضعیف اعداد بزرگ، تابع مولد گشتاور و کاربردهای آن، قضیه حد مرکزی.
توابع مختلط
ضرورت ارائهی درس
با ابداع دستگاه اعداد مختلط در اوایل قران بیستم، مفاهیم اصلی حسابان توابع یک متغیره حقیقی، یعنی مشتق و انتگرال، برای توابع مختلط، یعنی توابعی که دامنه و برد آنها زیرمجموعهای از اعداد مختلط است، مورد بررسی قرار گرفت. با توجه به قابلیتهایی که این دسته از توابع ایجاد میکردند، خیلی سریع این شاخه از ریاضیات به عنوان یکی از ابزارهای قدرتمند در شاخههایی از ریاضی همانند نظریه اعداد، هندسه جبری و فراکتالها مورد استفاده قرار گرفت. در سایر رشتهها نیز ابزار توابع مختلط توانایی بسیار خوبی از خود نشان داده، در مباحثی چون هیدرودینامیک و مکانیک کوانتم در فیزیک یا مباحث کنترل و مخابرات در مهندسی برق به کار گرفته شد. بر این اساس، آشنایی مقدماتی با مفاهیم مورد نیاز در این شاخه از ریاضیات برای دانشجویان کارشناسی ریاضی کاملا ضروری است.
شرح درس
دستگاه اعداد مختلط، اعمال جبری، فدر مطلق، مزدوج، نمایش قطبی اعداد مختلط، ریشههای اعداد مختلط، مفاهیم توپولوژیک مانند متریک و همبندی، توابع مقدماتی و خواص نگاشتی آنها، توابع تحلیلی و معادلات کوشی ریمان، توابع همساز، انتگرالگیری مختلط، قضیه کوشی-گورسات، فرمول انتگرال کوشی و کاربردهای آن، قضیه لیوویل، قضیهی اساسی جبر، سریهای توانی، سری تیلور، سری لوران، قضیه ماکزیمم کالبد، تکینها و صفرها، انواع تکینگیها، قضیه روشه، قضیهی هرویتس، حساب ماندههای کوشی و کاربرد آن در محاسبه انتگرالهای ناسره، تبدیلات خطی-کسری، نظریه نگاشتهای همدیس.
توپولوژی
ضرورت ارائهی درس
توپولوژی از مطالعه عمیقتر مفاهیم حساب دیفرانسیل و انتگرال و فضاهای متریک پدید آمده است. تلاشها برای دقیقتر کردن استدلالهایی که توسط نیوتن و لایبنیتز ارائه شده بودندو بر پایه شهود هندسی استوار بودند منجر به تعریف دقیق حد، صورت بندی آزمونهای همگرایی برای سریها و تعریف دقیق پیوستگی توابع گردید. با ارائه تعریف مجموعه توسط کانتور، این مفاهیم به صورتی مجرد پایههای اولیه توپولوژی را بنا نهاد. امروزه مطالعه توپولوژی به عنوان یک درس، علاوه بر اینکه به خودی خود جالب توجه است، پایههای مطالعه عمیقتر در حداقل نیمی از شاخههای ریاضی، از جمله هندسه، آنالیز ریاضی و توپولوژی جبری را فراهم میآورد.
شرح درس
فضاهای توپولوژیک، مجموعههای باز و بسته، همسایگی یک نقطه، نقطه درونی و نقطه حدی، بستار یک مجموعه، پایه و زیر پایه برای یک توپولوژی، فضای تفکیکپذیر، فضاهای شمارای نوع اول و دوم، فضای هاسدورف، توابع پیوسته، نگاشت باز، فضای حاصلضربی، قضیه تیخونوف و برخی کاربردهای آن مانند فشرده سازی اشتون-چک، نشاندن و همسانریختی، فضای خارجقسمتی و نگاشت خارجقسمتی، فشردگی و همبندی، اصول جداسازی، فضای منظم، فضای نرمال، لم اوریسون، فضاهای متری، قضایای متر پذیری و فرافشردگی، فضاهای متریک کامل، فضاهای تابعی، قضیه اسکولی.
توپولوژی جبری مقدماتی
ضرورت ارائهی درس
توپولوزی جبری یکی از گرایش های نسبتاَ جدید در ریاضی است که در قرن اخیر بعنوان ابزاری در حل مسائل بازِ شاخص در ریاضی کاربرد فراوان یافته است. این مطلب تا جایی اهمیت یافته است که مفاهیم آن حتی در شاخهای از ریاضیات گسسته یعنی گراف و ترکیبیات وارد شده است و برای حل مسائل این شاخه نیز مورد استفاده قرار گرفته است. لازم به ذکر است که گراف و ترکیبیات نه تنها در علوم ریاضی بلکه در رشته هایی از علوم مهندسی نظیر برق و کامیوتر بواسطه کارایی آن طرفداران زیادی دارد. بنابراین ارائه این درس در مقطع کارشناسی علاوه بر اینکه قدمی در به روز رسانی سیستم آموزشی دانشکده علوم ریاضی است، زمینه آشنایی دانشجویان علاقمند را به این گرایش فراهم میسازد.
شرح درس:
هموتوپی، هموتوپی توابع، بررسی خواص هموتوپی توابع ، فضاهای همارز هموتوپی، هموتوپی مسیری، هموتوپی مسیری بعنوان یک رابطه همارزی، فضای توپولوژی همراه با رابطه همارزی هموتوپی مسیری بعنوان یک شبه گروه، گروه بنیادی، تعیین گروه بنیادی فضاهای ساده، فضای پوششی و قضایای مربوط به آن، ترفیع مسیری و قضایای مورد نیاز ، تعیین گروه بنیادی دایره به کمک قضایای ترفیع مسیری ، نتایج حاصل از گروه بنیادی دایره نظیر نقطه ثابت برآور، تمایز دایره با کرههای با بعد بیشتر از یک، تمایز صفحه دو بعدی با فضاهای حقیقی با بعد بالاتر از دو، قضیه اساسی جبر، قضیه برسوک-اولام، گروه بنیادی فضاهای حاصلضرب.
جبر ۱
ضرورت ارائهی درس
جبر ابزاری دقیق و توانمند در ریاضیات است. در این مبحث از ریاضیات است که استدلالهای منطقی به بهترین وجه نمایان میشوند. میزان مستدل بودن هر علمی به درجه تبدیل مسالههای آن به مدلهای ریاضی بستگی دارد. نقش جبر در ریاضیات قابل قیاس با نقش ریاضیات در علوم است. بسیاری از ساختارهایی که در شاخههای مختلف علوم ریاضی ظاهر میشوند، در مبحث جبر به صورت انتزاعی مطالعه میشوند، که باعث پیشرفت هر دو شاخه میشود. در اولین برخورد با این درس دو مفهوم گروه و حلقه به صورت دقیق مطالعه میشوند. از آنجایی که این درس تقریبا در همهی درسهای علوم ریاضی به نوعی مطرح میشود و دروازهای به دروس نظری ریاضیات و علوم کامپیوتر است، اطمینان از درک صحیح دانشجویان از مفاهیم و قضایای آن کمک شایانی به فهم بهتر ریاضیات و کاربردهای آن میکند. تسلط دانشجویان بر این درس پایهی محکمی برای درسهای بعدی و تجربه با ارزشی برای مطالعه بیشتر اصل موضوعی در ریاضیات را فراهم میکند.
شرح درس:
مرور برخی خواص مجموعهها، روابط و توابع، اعمال دوتایی، رابطههای همارزی، مرور خواص اساسی اعداد صحیح، نیمگروه، تکوار، گروه، خواص مقدماتی گروه، مثالهایی از گروهها (گروه دووجهی، گروه چهارگان، گروه شبه دوری، ...)، جدول کیلی، معرفی و بررسی خواص گروههای مهم از قبیل گروه ردههای ماندهای به پیمانه n و گروه جایگشتها روی n حرف، زیرگروه، زیرگروههای مهم یک گروه، مرکزساز یک عضو، مرکز، نرمالساز یک زیرگروه، گروه دوری، ساختار گروههای دوری، مرتبهي یک عضو، تولید گروهها، گروه متناهی تولید، هممجموعهها، شاخص یک زیرگروه، معادلهی ردهای و کاربردهای آن، قضیهی لاگرانژ، زیرگروههای نرمال، ساده بودن گروه متناوب، گروههای خارج قسمتی، قضیهی کُشی، همریختی، گروه خودریختیهای یک گروه دوری، قضایای یکریختی، ساختار گروههای آبلی متناهی، حلقه، خواص مقدماتی حلقهها، حلقهی ماتریسها، مقسوم علیه صفر، اعضای وارونپذیر، اعضای پوچتوان و خودتوان، دامنهی صحیح، زیرحلقه، همریختی، ایدآل، حلقهی خارج قسمتی، قضایای یکریختی، حلقهی کسرهای یک دامنهی صحیح، مرور مختصر حلقهی چندجملهایها، چندجملهایهای تحویلناپذیر، تجزیهی چندجملهایها روی یک میدان.
جبر خطی ۱
ضرورت ارائهی درس
جبر خطی از مهمترین مباحث در ریاضی است. در این مبحث ماتریسها، دستگاه معادلات خطی، فضاهای برداری، تبدیلهای خطی مطالعه میشوند. کاربردهای نظری و عملی بسیار زیاد، جبر خطی را به شاخهای جذاب از ریاضی تبدیل کرده است. کمتر شاخهای از ریاضیات را میتوان یافت که از جبر خطی استفاده نکند. این اهمیت باعث شده درس جبر خطی درس پایهای برای برخی از رشتههای کارشناسی و تحصیلات تکمیلی علوم و مهندسی مطرح باشد. در اولین برخورد با جبر خطی لازم است علاوه بر آماده سازی دانشجو برای درک مفاهیم نظری، جنبههای کاربردی و محاسباتی آن نیز مورد توجه قرار گیرد. برای اولین درس بهتر است برخی مفاهیم نظری سادهتر ارائه و از اثباتهای نظری پیچیده و مشکل صرفنظر کرد.
شرح درس:
ماتریسها و اعمال جبری روی آنها، دستگاه معادلات خطی، اعمال سطری مقدماتی، ماتریسهای سطری پلکانی تحویل یافته، رتبه ماتریس، محاسبه وارون یک ماتریس، دترمینان و خواص مقدماتی آن، فضاهای برداری و خواص آنها، مثالهای مهم فضاهای برداری، زیرفضا، استقلال و وابستگی خطی، پایه و بعد، جمع زیرفضاها، فضاهای ضرب داخلی، قضیهی گرام-اشمیت، تجزیهی متعامد، تبدیلهای خطی، ماتریس یک تبدیل خطی، ماتریس تبدیل پایه، رتبه و پوچی تبدیل خطی، مقادیر و بردارهای ویژه، چندجلهای سرشتنما، چندجملهای مینیمال، قضیه تجزیه اولیه یا طیفی، قضیه کیلی همیلتون، فرمهای مثلثی، فرمهای ژردان.
دستگاههای دینامیکی گسسته
ضرورت ارائهی درس
برای متخصصین بسیاری از علوم، به خصوص فیزیک و مهندسی، لزوم شناخت نظریه و رفتارهای کیفی (دینامیکهای) مدلهای مربوط به پدیدههای در حال تکرار با زمان های گسسته (ماه، فصل، سال و ...) روشن است. از سوی دیگر یک روش بررسی رفتارهای برخی جوابهای معادلات دیفرانسیل استفاده از دستگاههای دینامیکی زمان-گسسته است. بنابراین به طور خاص برای یک دانشجوی رشته ریاضی ضروریست تا با مبانی نظری و کاربردهای دستگاههای دینامیکی زمان-گسسته آشنا شود. همچنین همتراز با بسیاری از دانشگاههای مطرح دنیا، ارائه یک درس برای آموزش مبانی دستگاههای دینامیکی زمان-گسسته به عنوان یکی از شاخههای پر اهمیت ریاضی لازم است.
شرح درس:
معرفی دستگاههای دینامیکی گسسته به صورت نگاشتها و معادلات تفاضلی، برخی مدلهای جمعیتی به عنوان دستگاههای دینامیکی گسسته، روابط بین معادلات دیفرانسیل و دستگاههای دینامیکی گسسته، معرفی برخی نگاشتهای مهم دستگاههای دینامیکی گسسته مثل نگاشت لجستیک و نگاشت خیمه، نگاشتهای دایرهای، مدار، نقاط ثابت و نقاط تناوبی، پایداری نقاط ثابت و تناوبی، بررسی کامل نگاشتهای مربعی شامل نقاط ثابت و نقاط تناوبی و دامنه جذب آنها و معرفی انشعابهای مضاعفساز دوره تناوب، قضیه شارکوسکی، تعریف آشوب از دیدگاه دیوینی و استقلال شرایط آن، نگاشتهای مزدوج، مجموعههای کانتور، دینامیکهای نمادین، اثبات آشوب برای نگاشت اولام و نگاشتهای لجستیک با پارامتر بزرگتر از ۴، نگاشتهای چند بعدی همراه با پایداری نقاط ثابت، قضیه هارتمن-گروبمن، قضیه منیفلدهای پایدار و ناپایدار و مرکزی، نگاشتهای انتقال دو طرفه، نگاشت نعل اسب و اثبات آشوب برای آن، نگاشت هنون و ویژگیهای آن، خودریختیهای چنبرهای هذلولوی، انشعابهای گره زینی، تبادل پایداری، چنگال و مضاعفسازی دوره تناوب.
رگرسیون ۱
تعداد واحد/ساعت: ۳ واحد
پیش نیاز: همنیاز با آمار ریاضی
حل تمرین: حداقل ۱۷ ساعت
از جدول:
- لازم است حداقل 1 واحد از درس به صورت عملی و از طریق تدریس و کار کردن با نرم افزار مشخص در سر کلاس درس باشد و یک سوم نمره نهایی دانشجویان نیز بر این اساس تعیین شود.
سر فصل درس و ریزمواد:
- تعریف مدلسازی آماری و بیان تفاوت آن با مدلسازیهای غیر آماری، ذکر جایگاه مدلهای رگرسیونی و کاربردهای آن، بیان تفاوت مدلهای رگرسیون خطی و غیرخطی
- رگرسیون خطی ساده: معرفی مدل رگرسیون خطی ساده، برآورد کمترین مربعات پارامترها، خواص برآوردگرها ، برآورد 2، تفسیر ضرایب رگرسیونی
- بیان الگوی تفکیک جامعیت به چندین زیرجامعیت متناظر با هر الگو از متغیرهای توضیحی و سپس مطرح کردن فرضیات رگرسیون خطی در این چارچوب، آزمون فرض در رابطه با ضرایب رگرسیونی، برآورد فاصلهای برای ضرایب رگرسیونی، برآورد فاصله ای میانگین پاسخ، پیش بینی مشاهدات جدید، فاصله پیش بینی مشاهده جدید، تفسیر ضرایب رگرسیونی
- تعریف ضریب تعیین، رگرسیون عبوری از مرکز، برآورد ماکزیمم درستنمایی، تعریف ضریب همبستگی و آزمون آن، مدل رگرسیونی با متغیرهای توضیحی تصادفی
- یادآوری مفاهیم جبرخطی مرتبط با مدلهای رگرسیونی
- رگرسیون خطی چندگانه: معرفی مدلهای رگرسیون خطی چندگانه، برآورد پارامترها به روش کمترین مربعات خطا، خواص برآوردگرها، برآورد 2
- برآورد فاصلهای برای ضرایب رگرسیونی، برآورد فاصله ای میانگین پاسخ، مدلهای رگرسیونی با ماتریس مدل با ستونهای متعامد، پیشبینی مشاهدات جدید به صورت نقطهای و فاصلهای، برون افتادگی مخفی، ضرایب رگرسیونی استاندارد شده، ضریب تعیین چندگانه، اشاره کوتاهی به مدلهای رگرسیونی چند جملهای
- آزمون فرضیه: آزمون معناداری رگسیون خطی، آزمون ضرایب رگرسیون جزیی، آزمون صفر بودن زیر مجموعهای از ضرایب رگرسیونی، تعمیم آزمون فرضیه خطی کلی
- متغیرهای توضیحی نشانگر در رگرسیون خطی ساده: تفسیر ضرایب رگرسیونی، استفاده از متغیرهای نشانگر در مقابل متغیرهای کدگزاری شده، استفاده از متغیرهای نشانگر در مقایسه بین دو خط رگرسیونی برازش داده شده بین متغیرها در دو جمعیت
مراجع:
- مقدمهای بر تحلیل رگرسیون خطی، د. مونتگومری و ا. پک، ترجمه رضوی پاریزی، انتشارات دانشگاه شهید باهنر کرمان، چاپ چهارم، 1390
- مدلهای خطی برای آمار، ا. رنچر، ترجمه ح. آذرنوش و ا. بزرگ نیا، انتشارات دانشگاه فردوسی مشهد، چاپ دوم، 1386
رگرسیون ۲
تعداد واحد/ساعت: ۳ واحد
پیش نیاز:
حل تمرین: حداقل ۱۷ ساعت
- لازم است حداقل 1 واحد از درس به صورت عملی و از طریق تدریس و کار کردن با نرم افزار مشخص در سر کلاس درس باشد و یک سوم نمره نهایی دانشجویان نیز بر این اساس تعیین شود.
سرفصل درس و ریز مواد:
- یادآوری از مدلهای رگرسیون خطی
- انتخاب مدل: نتایج کم برازش و بیش برازش در اثر ورود متغیرهای توضیحی ناکافی در مدلهای رگرسیون خطی ، روشهای انتخاب متغیر مانند انتخاب پیشرو، حذف پسرو و روش قدم به قدم،
- بیان همخطی چندگانه: تعریف آن، بیان مشکلات ایجاد شده توسط آن، روشهای تشخیص آن، دلایل ایجاد آن و نحوه برخورد با آن
- معیارهای مناسبت مدل: معرفی انواع باقیماندهها در مدلهای رگرسیون خطی، معرفی دادههای دورافتاده، اهرمگون و تاثیرکذار و بیان تاثیرگذاری این دادهها بر مدل و نحوه تشخیص و برخورد با آنها، بررسی فرضیه نرمال بودن توزیع خطاها، بررسی فرضیه ثبات واریانس در مدلها، رگرسیون وزنی، آزمون کمبود برازش خطی، انتخاب تبدیل مناسب جهت برقراری فرضیه نرمال بودن و یا تثبیت واریانس.
- ذکر محدودیتهای مدلهای رگرسیون خطی، تعریف خانواده توزیعهای نمایی و بیان خواص آنها، تعریف مدلهای رگرسیون خطی تعمیمیافته (GLM)
- روش برآورد ماکزیمم درستنمایی پارامترها در GLMها، معرفی توزیع حدی و خواص برآوردگرها، معرفی آماره انحراف (Deviance) و توزیع حدی آن، محاسبه آماره انحراف در مدلهای رگرسیون خطی، رگرسیون لجستیک و مدلهای لگ-خطی،
- آزمون فرضهای ضرایب رگرسیونی با استفاده از روشهای تفاضل انحرافات، آماره والد و آماره امتیاز
- مدلهای رگرسیونی برای متغیرهای پاسخ دودویی: معرفی انواع توابع پیوند، معرفی آماره های نیکویی برازش، معرفی انواع باقیماندهها، معرفی مساله بیش پراکنش و بیان روشهای تشخیص و برخورد با این مساله، تفسیر ضرایب رگرسیونی
- مدلهای رگرسیونی برای متغیرهای پاسخ شمارشی: معرفی انواع توابع پیوند، معرفی آمارههای نیکویی برازش، معرفی انواع باقیماندهها، معرفی مساله بیش پراکنش و بیان روشهای تشخیص و برخورد با این مساله، تعریف offset در این مدلها، تفسیر ضرایب رگرسیونی، بیان مدلهای رگرسیونی جهت تحلیل دادههای خلاصه شده در جداول توافقی
- معرفی مدلهای رگرسیونی متداول جهت تحلیل متغیرهای پاسخ اسمی و ترتیبی، تفسیر ضرایب رگرسیونی
مراجع:
- مقدمهای بر تحلیل رگرسیون خطی، د. مونتگومری و ا. پک، ترجمه رضوی پاریزی، انتشارات دانشگاه شهید باهنر کرمان، چاپ چهارم، 1390
- مدلهای خطی برای آمار، ا. رنچر، ترجمه ح. آذرنوش و ا. بزرگ نیا، انتشارات دانشگاه فردوسی مشهد، چاپ دوم، 1386
A.J. Dobson and A. Barnet, An Introduction to Generalized Linear Models, Third Ed., (2008) Chapman and Hall/CRC.
روش های نمونه گیری ۱
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیش نیاز: آمار ریاضی ۱
حل تمرین: حداقل 25
از جدول:۳
سرفصل درس و ریز مواد:
- مقدمه ای بر آمارگیری های نمونه ای: مفهوم نمونه گیری و سرشماری ، نمونه گیری نااحتمالاتی، نمونه گیری احتمالاتی، چارچوب نمونه گیری، پارامترهای جامعه،
- مفاهیم پایه در نمونه گیری: توزیع جامعه، فرآیند پاسخ گویی، جامعه نمونه گیری شده، خطای کل آمارگیری؛ خطای نمونه گیری و خطای غیرنمونه گیری
- نمونه گیری تصادفی ساده: گزینش نمونه (بدون جایگذاری و با جایگذاری)، برآوردگرهای پارامترهای جامعه (کل، میانگین و نسبت)، توزیع نمونه ای برآوردگرها: معیارهای کیفیت برآوردگرها (اریبی، واریانس)، بازه های اطمینان، تعیین اندازه ی نمونه.
- نمونه گیری طبقه بندی شده: برآوردگرهای کل، میانگین و نسبت، انتخاب طبقه ها، تعیین اندازه نمونه، انواع تخصیص حجم نمونه به طبقه ها، مقایسه نمونه گیری تصادفی ساده و طبقه ای، طبقه بندی پسین
- نمونه گیری با احتمالات متغیر: نمونه گیری با احتمالات متناسب با اندازه، شیوه انتخاب نمونه با احتمال متغیر، روش های انتخاب نمونه به صورت با جایگذاری (لاهیری و تجمعی)، نمونه گیری با احتمال متغیر بدون جایگذاری ، برآوردگرهای کل، میانگین ونسبت
مراجع:
- عمیدی, علی، نظریه نمونه گیری و کاربردهای آن، چاپ سوم، 1384، مرکز نشر دانشگاهی، تهران
- مقدمه ای بر بررسی های نمونه ای، چاپ چهارم، 1384، ترجمه ناصر رضا ارقامی، ناهید سنجری فارسی پور، ابوالقاسم یزرگ نیا، انتشارات دانشگاه فردوسی مشهد
- C. E. Sarndal, B. Swensson, J. Wretman, Model Assisted Survey Sampling,
- W. G. Cochran, Sampling Techniques, John Wiley & Sons, Inc. New York, 1977.
روش های نمونه گیری ۲
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیش نیاز: نمونه گیری ۱
حل تمرین: حداقل ۲۵
از جدول: ۳
سرفصل درس و ریز مواد:
- برآوردگر نسبتی برای برآورد میانگین جامعه، برآوردگر شبه نسبتی (برآورد هارتلی-راس)، برآوردگر رگرسیونی
- نمونه گیری سیستماتیک: روش های گزینش نمونه؛ حالت بخشپذیری Nبر n، روش دوری، روش کسری ، تعیین برآوردگرها
- نمونه گیری خوشه ای یک مرحله ای: نمونه گیری خوشه ای یک مرحله ای از جامعه با خوشه های هم حجم، نمونه گیری خوشه ای یک مرحله ای از جامعه با خوشه های با حجم نابرابر، نمونه گیری خوشه ای یک مرحله ای با احتمال متغیر و با جایگذاری، برآورد پارامترها( کل، میانگین و نسبت)، مقایسه نمونه گیری خوشه ای و تصادفی ساده
- نمونه گیری خوشه ای دو مرحله ای: روشهای انتخاب نمونه؛ حالتی که هر دو مرحله به شیوه تصادفی ساده باشند، حالتی که مرحله اول به شیوه نمونه گیری با احتمال متغیر و با جایگذاری باشد، برآورد پارامترها (کل، میانگین و نسبت)
مراجع:
- عمیدی, علی، نظریه نمونه گیری و کاربردهای آن، چاپ سوم، 1384، مرکز نشر دانشگاهی، تهران
- مقدمه ای بر بررسی های نمونه ای، چاپ چهارم، 1384، ترجمه ناصر رضا ارقامی، ناهید سنجری فارسی پور، ابوالقاسم یزرگ نیا، انتشارات دانشگاه فردوسی مشهد
- C. E. Sarndal, B. Swensson, J. Wretman, Model Assisted Survey Sampling,
- W. G. Cochran, Sampling Techniques, John Wiley & Sons, Inc. New York, 1977.
روشهای آماری
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیش نیاز: احتمال ۱
حل تمرین: حداقل ۱۷ ساعت
سر فصل درس و ریزمواد:
در این درس مفاهیم آماری به کمک یک نرم افزار شرح داده می شود.
- نمونه تصادفی، توزیعهای نمونهای و قضیه حد مرکزی
- تعریف پارامتر جامعه (میانگین - واریانس - نسبت) - برآوردیابی نقطهای - ملاکهای انتخاب برآوردگر مناسب (نااریبی - کارایی -MSE)
- برآوردیابی فاصلهای - روش کمیت محوری - تعابیر برآورد فاصلهای - برآوردفاصلهای با اندازه نمونه بزرگ
- برآوردیابی فاصلهای برای تفاضل میانگینها و نسبتها و نسبت واریانسها در دو جامعه
- آشنایی مقدماتی با مفاهیم آزمون فرض (نحوهی صورتبندی فرضها) - آزمون فرضهای ساده - معرفی آماره آزمون - قاعده تصمیم گیری - خطاهای نوع اول و دوم - آزمون فرضهای یکطرفه و دوطرفه (برای پارامترهای میانگین، واریانس و نسبت جامعه)، معرفی p-مقدار - آزمون فرضها با اندازهی نمونه بزرگ
- آزمون فرضها برای مقایسه تفاضل میانگینها و نسبتها و نسبت واریانسها برای دو جامعه مستقل (اندازه نمونه کوچک و بزرگ)
- استنباط آماری در مورد تفاضل میانگینهای مشاهدات زوجی
- آزمون نیکویی برازش- جداول توافقی: استقلال و همگنی
- مفهوم همبستگی خطی و رگرسیونخطی ساده
مراجع:
- کتاب مفاهیم و روشهای آماری باتاچاریا، ترجمه شهرآشوب (جلد اول و دوم)
- بهبودیان، جواد، آمار و احتمال مقدماتی، چاپ شانزدهم، آستان قدس رضوی 1383.
- پارسیان، احمد، مبانی احتمال و آمار برای دانشجویان علوم و مهندسی، ویرایش دوم، چاپ دوم، مرکز نشر دانشگاه صنعتی اصفهان، 1388.
- چ ووناکات، ت،جی، ووناکات، آمار مقدماتی، ترجمه محمدرضا مشکانی، چاپ پنجم، مرکز نشر دانشگاهی تهران،1382.
- Mendenhall, Beginning Statistics A to Z, 1993
روشهای چند متغیره گسسته
تعداد واحد/ساعت: 3 واحد
پیش نیاز: هم نیاز با آمار ریاضی
حل تمرین: حداقل 17
از جدول:
- حل تمرین 1ساعت در هفته شامل آزمایشگاه باشد.
سر فصل درس و ریزمواد:
- مفاهیم اولیه: معرفی متغیرهای تصادفی گسسته(دودویی، شمارشی، رتبهایی، اسمی و ...) و توزیعهای نمونه ایی متداول در این درس (برنولی، دوجملهایی، پواسون، چندجمله ایی و فوق هندسی) استنباط های مورد نیاز در توزیعهای فوق: برآوردگرهای ماکسیمم درستنمایی (و خواص مجانبی) ، فاصله اطمینان، آزمون فرض (آمارههای نسبت درستنمایی، پیرسون، والد و امتیاز)
- جدولهای پیشایندی (دو طرفه- سه طرفه) تعریف جدول پیشایندی (به عنوان ابزاری جهت خلاصه کردن دادهها) ، انواع روشهای نمونه گیری در این جدولها ( مشخص بودن تعداد کل مشاهدات، جمعهای حاشیه ایی سطری معلوم و مشخص نبودن تعداد کل مشاهدات) ، مقایسه نسبتها به کمک پارامترهای پیوند شامل: تفاضل نسبت، مخاطره نسبی و نسبت بختها ( استنباط درباره این پارامترها مانند برآورد نقطهایی، فواصل اطمینان مجانبی و آزمون فرض)
- استنباط در جدولهای پیشایندی بیان مفاهیم و تعابیر انواع پارامترهای پیوند و استقلال در جدولهای دو و سه طرفه، آزمون انواع استقلال در نمونه بزرگ ( به کمک آمارههای نسبت درستنمایی، پیرسون، والد و امتیاز) و تقریبهای نمونه بزرگ. آزمون استقلال در جدولهای پیشایندی با حجم نمونه کوچک: آزمون دقیق فیشر، بیان معایب و ارائه راهکار مانند آزمون تصادفیده و
 -مقدار معرفی معیار پیوند دیگر در دادههای رسته ایی (مانند
-مقدار معرفی معیار پیوند دیگر در دادههای رسته ایی (مانند  - کندال و
- کندال و  -کرامر) ، معیار پیوند در دادههای ترتیبی.
-کرامر) ، معیار پیوند در دادههای ترتیبی. - مدلهای خطی تعمیم یافته
مدل کردن پارامتر نسبت به کمک یک مدل خطی و بیان محدودیتها و معایب، معرفی مدل خطی تعمیم یافته و مولفههای آن، مدل خطی تعمیم یافته در پاسخهای دودویی و پاسخهای شمارشی، برازش مدل به دادهها، استنباط پارامترهای مدل و بیان معیار(های) نیکویی برازش.
- رگرسیون لوژستیک
مدل در حضور چند متغیر پیشگو، مدل اشباع شده، استنباط درباره پارامترهای مدل و تعبیر آنها ( بیان مجدد مفهوم پارامتر نسبت بخت و ارتباطش با پارامترهای مدل) ، معیارهای نیکویی برازش و انتخاب مدل.
- مدل لگ-خطی در دادههای شمارشی
مدلهای لگ-خطی در جدولهای دو و سه طرفه، بیان انواع استقلالها به کمک مدل لگ-خطی، استنباط در مدلهای خطی تعمیم یافته، آزمون نیکویی برازش (آزمون کای دو و بررسی باقیماندههای سلولی) ، آزمون استقلال و تقلیل بعد، آزمونهای استقلال شرطی و فواصل اطمینان مرتبط با نسبتهای بخت شرطی
مراجع:
- A. Agresti, An Introduction to Categorical Data Analysis,John Wiley, 1996.
- Dobson, A., An Introduction to Generalyzed Linear Models, 2th Ed. Chapmann & Hall, 2002.
روشهای مقدماتی آمار
سر فصل درس و ریزمواد:
- معرفی کاربردهای آمار در رشته های مختلف وسپس بیان مفاهیم جمعیت ،نمونه و داده های پیوسته وگسسته با مثال
- معرفی یک نرم افزار و استفاده از آن برای انجام کارهای توصیفی آماری ،به شرح بندهای بعد و به صورت عملی
- جداول آماری: هیستوگرام، نمودار دایره ای، چندبر فراوانی مطلق و تجمعی، منحنی های فراوانی مطلق و تجمعی، نمودار شاخه و برگ، نمودار جعبه ای
- معیارهای مرکزی شامل میانگین حسابی، هندسی، وزنی، توافقی، ریشه ای، میانه، مد، چندکها، چارکها، دهکها، صدکها
- معیارهای پراکندگی شامل دامنه، دامنه میان چارکی، میانگین انحراف از میانگین، میانگین انحراف از میانه، واریانس، انحراف معیار، ضریب تغییرات
- خواص منحنی فراوانی شامل تک نمایی، تقارن، چولگی، برجستگی
- آنالیز دادهها بر اساس آموزشهای گذشته
مراجع:
- آمار راهی به سوی ناشناخته ها،
- آمار و احتمال مقدماتی، بهبودیان، جواد، چاپ شانزدهم، 1383، انتشارات آستان قدس رضوی.
- آمار مقدماتی، اچ ووناک، تی. جی. ووناک، ترجمه محمدرضا مشکانی، چاپ پنجم، 1382، مرکز نشر دانشگاهی، تهران.
- مرجعی مناسب برای آموزش نرم افزار
امكانات لازم: مکان استفاده از کامپیوتر و نرم افزارهای آماری در آزمایشگاه برای همه دانشجویان ضرورت ارائه درس: این درس به عنوان اولین درسی که دانشجویان رشته آمار اخذ مینمایند آنها را برای شروع تحصیل در این رشته آماده میکند. با نرم افزاری که بعدها نیاز دارند آشنا میکند و آمار توصیفی را که در دروسه دیگر تنها از آن استفاده میکنند ولی تدریس نمیشود به طور کامل تدریس میشود. شرح درس: معرفی کاربردهای آمار در رشته های مختلف وسپس بیان مفاهیم جمعیت ،نمونه و داده های پیوسته وگسسته با مثال، معرفی یک نرم افزار و استفاده از آن برای انجام کارهای توصیفی آماری ،به شرح بندهای بعد و به صورت عملی، جداول آماری: هیستوگرام، نمودار دایره ای، چندبر فراوانی مطلق و تجمعی، منحنی های فراوانی مطلق و تجمعی، نمودار شاخه و برگ، نمودار جعبه ای، معیارهای مرکزی شامل میانگین حسابی، هندسی، وزنی، توافقی، ریشه ای، میانه، مد، چندکها، چارکها، دهکها، صدکها، معیارهای پراکندگی شامل دامنه، دامنه میان چارکی، میانگین انحراف از میانگین، میانگین انحراف از میانه، واریانس، انحراف معیار، ضریب تغییرات، خواص منحنی فراوانی شامل تک نمایی، تقارن، چولگی، برجستگی، آنالیز دادهها بر اساس آموزشهای گذشته.
Course Discription: Introduction to the application of statistics in different fields, Definition of statistical population, random sample and data set (continous and discrete) with examples. Using a statistical software in laboratory to teach statistical methods, Descriptive statistics; graphical and numerical representation of information, statistical tables, histogram, statistical graphs,….skewness, and data analysis.
|
ریاضی گسسته
ضرورت ارائهی درس
هدف اصلی این درس آشنا نمودن دانشجویان با مفاهیم اصلی و پایه ای در ترکیبیات و ریاضیات گسسته است به نحوی که در عین آشنایی با این مفاهیم با کاربردها و انگیزه های اصلی که در علم ترکیبیات وجود دارد آشنا شده و با برخی مسائل اصلی آن نیز روبهرو شوند. در این راستا و با توجه به محتوی و نوع این درس، اهداف دیگری نیز میتوانند در این درس پیگیری شوند که عبارتند از:
الف) تمرین ارائه استدلالهای دقیق ریاضی و انواع مختلف آنها (نظیر: استقراء ریاضی، برهان خلف و ...)
ب) آشنایی با استدلالهای ترکیبیاتی (نظیر: استدلالهای مبتنی بر شمارش، وضعیت بحرانی،...)
ج) آشنایی با ساختارهای مختلف گسسته (نظیر: مجموعههای متناهی، روابط متناهی، ماتریسها، گرافها، مربعهای لاتین و...)
د) تمرین ارائه استدلالهای مبتنی بر تفکر الگوریتمیک و آشنایی با الگوریتمهای مختلف درحوزه ترکیبیات.
شرح درس:
روشهای شمارش، اصول اساسی شمارش، اصل لانه کبوتری، شمارش دوگانه، جایگشتها و ترکیبها، ضرایب دوجملهای، اصل شمول و عدم شمول، روابط بازگشتی، روشهای حل روابط بازگشتی، توابع مولد معمولی و نمایی، ماتریسها، ماتریسها از دیدگاه ترکیبیاتی، برخی خواص مهم ماتریسهای صفر و یک، معرفی مفاهیم اولیه نظریه گراف و مدلهای مبتنی بر آنها، معرفی مفهوم گراف با تأکید بر کاربردهای آن در مدلسازی، آشنایی با مفاهیم اصلی نظریه گراف، درجه، دنباله درجه، انواع اصلی گراف نظیر دور، مسیر، گرافهای کامل، درختها، گرافهای دوبخشی، گرافهای اویلری و هامیلتونی، گرافهای جهتدار و تورنمنتها، تطابقهای کامل و ماکزیمم، رنگآمیزی گرافها، گرافهای مسطح، مربعهای لاتین، طرحها و هندسههای متناهی، تعاریف و مفاهیم اصلی با تأکید بر ارتباط این مفاهیم، ارائه مثال و کاربرد در مربع های لاتین و چند کاربرد، سیستمهای نمایندگی متمایز (SDR)، قضیه فیلیپ هال.
سریهای زمانی ۱
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیش نیاز: احتمال ۲/ فرایندهای تصادفی ۱ (هم نیاز)
حل تمرین: حداقل ۱۷ ساعت
سر فصل درس و ریزمواد:
- مقدمه، تعریف سری زمانی و مثالهای کاربردی از سریهای زمان گسسته و زمان پیوسته با وضعیت پیوسته و گسسته و بیان هدف و اهمیت آنالیز سریهای زمانی
- تغییرات مختلف سریهای زمانی مخصوصا تغییرات ایستا، اثرات روند، اثرات فصلی و براورد و حذف آنها
- مدلهای ایستای اکید و ایستای درجه دو
- تابع میانگین، تابع خودهمبستگی و تعبیر نمایش هندسی آن
- نوفه سفید و نوفه مستقل همتوزیع و آزمونهای تشخیص آنها
- مدلهای معروف خطی در فرایندهای ایستا از جمله MA، AR، ARMA و مثالهای از هر کدام
- قضیه تجزیه والد
- پیش بینی در مدلهای خطی معرفی شده
- مدلبندی با دادههای واقعی
- براورد تابع میانگین و تابع خودهمبستگی
- براورد پارامترهای سری با مدل خطی
- تعیین درجه مدل و تشخیص مدل
- معرفی مقدماتی مدلهای ناایستا
مراجع:
- Introduction to Time Series and Forecasting, Peter J. Brockwell & Richard A. Davis, 2th ed., 2010.
- Introduction to Statistical Time Series, Wayne A. Fuller, J. Wiley & Sons, 1979.
طرح و تجزیه آزمایش ۱
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
سر فصل درس و ریزمواد:
- مقدمه: مقدمه ای بر طرح آزمایش ها و کاربرد آن – مراحل طراحی یک آزمایش – اصول پایه
- آزمایش های تک عاملی: طرح کاملا تصادفی شده – تحلیل مدل اثرهای تثبیت شده و برآورد پارامترها ی مدل – قضیه کاکران – یافتن امید ریاضی میانگین مربعات – یافتن آماره آزمون و ناحیه بحرانی با استفاده از امید ریاضی میانگین مربعات
جدول آنالیز واریانس – طرح های نامتعادل – مقایسه چندگانه میانگین ها ی تیماری– آزمون مقابله ها ی تیماری – مقابله های متعامد چند روش برای مقایسه همزمان همه مقابله های تیماری – مدل اثرهای تصادفی و یافتن جدول آنالیز واریانس برای آن – مقایسه مدل اثرهای تثبیت شده با مدل تصادفی – طرح اندازه های مکرر
- کفایت مدل: :بررسی کفایت مدل – پذیره نرمال و مستقل بودن خطاها– خطی بودن مدل – واریانس ثابت – تحلیل مانده ها – نمودار احتمال نرمال – انتخاب اندازه نمونه – منحنی های مشخصه عملکرد (OC)
- طرح های بلوکی کامل: طرح بلوکی کامل تصادفی شده – یافتن آماره آزمون و ناحیه بحرانی با استفاده از امید ریاضی میانگین مربعات –جدول آنالیز واریانس مقایسه چندگانه میانگین ها ی تیماری – برآورد پارامترهای مدل – بررسی مناسبت مدل – برآورد داد ه های گمشده – تعیین اندازه بلوک با استفاده از منحنی های مشخصه عملکرد – طرح مربع لاتین و طرح مربع یونانی-لاتین همراه با جدول آنالیز واریانس آنها
- طرح های بلوکی ناقص: طرح بلوکی ناقص متعادل و تجزیه و تحلیل آن – برآورد پارامترهای مدل با روش کمترین مربعات خطا– طرح بلوکی ناقص بطورجزئی متعادل – طرح مربع یودن
در این درس با استفاده از نرم افزار آماری S-Plus یک پروژه انجام می شود.
مراجع :
- Design and Analysis of Experiments, D. C. Montgomery, 2001, 5th ed.
طرح و تجزیه آزمایش ۲
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
سر فصل درس و ریزمواد:
مبانی طرح های عاملی: اصول و تعاریف - طرح های عاملی با دو عامل – بررسی مدلهای طرح دوعاملی در دو حالت با و بدون اثر متقابل – یافتن امید ریاضی میانگین مربعات ساختن آماره آزمون با استفاده از آنها – جدول آنالیز واریانس – مقایسه چندگانه میانگین ها ی تیماری– آزمون مقابله های تیماری – تجزیه و تحلیل طرح های 2 عاملی با یک تکرار – اندازه نمونه – مدلهای تصادفی و آمیخته و مقایسه جدول آنالیز واریانس آنها – تعمیم طرح های 2عاملی به طرح های عاملی با 3 عامل و بیشتر– بررسی کفایت مدل و تحلیل مانده ها
- طرح های عاملی 2k: کدبندی ترکیبهای تیماری در طرح 22– یافتن مقابله های تیماری و رابطه آنها با مجموع مربعات و برآورد اثرها – آنالیزواریانس با روش های خاص در طرح های 22– برازش مدل رگرسیونی و تحلیل مانده ها – طرح های 23–تعمیم روشهای تجزیه و تحلیل طرح های 22 بهطرح های 23– طرح عاملی کلی 2k– طرح های تک تکراری و روشهای مختلف تجزیه و تحلیل آنها– تصویر کردن طرح های تک تکراری – الگوریتم یتس
- مخلوط کردن طرح های عاملی 2k: مفهوم مخلوط کردن – مخلوط کردن در دو بلوک – روشهای مختلف مخلوط کردن – مقابله های معرف– تکرار بلوک ها – مخلوط کردن جزئی – مخلوط کردن در چهار بلوک – خواص و رابطه بین بلوک ها – مخلوط کردن درتعداد 2p بلوک
- طرح عاملی کسری دو سطحی : کسر یک دوم طرح 2k – مولد ها و رابطه معرف طرح کسری – هم اثرها – وضوح (تجزیه) طرح های کسری – روش ساختن طرح کسر یک دوم– بکار بردن آلگوریتم یتس برای یافتن برآورد اثرها و مجموع مربعات – کسر یک چهارم طرح 2kو روش ساختن آن – بررسی طرح عاملی کسری کلی 2k-p– تعمیم نتایح کسر یک چهارم به طرح های کسری کلی – بلوك بندی طرح های كسری – طرح های کسری با وضوح III و IV وV– طرح های اشباع شده – تا کردن طرح های کسری – جداسازی برآورد اثرها – رابطه معرف برای طرح های تا شده
- تحلیل کوواریانس: مقدمه – طرح های تک عاملی با یک متغیر تصادفی کمکی – آنالیز کوواریانس – تحلیل مانده ها
- در این درس با استفاده از نرم افزار آماری S-Plus یک پروژه انجام می شود.
مراجع :
- Design and Analysis of Experiments, D. C. Montgomery, 2001, 5th ed.
فرآیندهای تصادفی
در چند دهه اخیر مشخص شده است که مدلهای واقعی پدیدههای طبیعی، مدلهایی هستند که نقش عوامل تصادفی در آنها موثر است و معمولا مدلهای غیر تصادفی که به مدلهای تعینی معروف می باشند، چندان مناسب مدل سازی نمی باشند. بر همین اساس بخشهایی از علوم ریاضیات و علوم دیگر که هدف آنها مدلسازی پدیدههای طبیعی است، برای یافتن مدلهای واقعی به در نظر گرفتن مدلهای تصادفی نیازمند هستند. از اینرو شناخت و آشنایی با ریاضیات تصادفی بسیار درخور توجه است. از کاربردهای مختلف آن میتوان به کاربرد آن در ریاضیات زیستی، ریاضیات مالی، حل معادلات نویر-استوکس، گرافهای تصادفی، شبکه، مخابرات، طراحی، بیمه، آیرودینامیک و ... اشاره کرد.
در این درس به معرفی فرآیندهای تصادفی زمان ـ پیوسته و زمان ـ گسسته پرداخته می شود که شامل فرآیندهای برنولی، فرآیندهای پواسون (اعم از پواسون، پواسون مرکب، پواسون ناپایا و ...)، زنجیرهای مارکوف و فرآیندهای مارکوف زمان ـ پیوسته می باشد.
پیشنیاز این درس:
دروس احتمال ۱ و ۲ یا دروس معادل با آن ( احتمال و کاربردها، احتمال مهندسی و آمار احتمال مهندسی)
منابع بسیار زیادی برای این درس نوشته شده است که در ادامه به برخی از آنها اشاره می شود:
- Cinlar, E. (1975) Introduction to Stochastic Processes. Prentice Hall, Englewood Cliffs, NJ.
- Durrett, R. (2016) Essentials of Stochastic Processes. Springer Texts in Statistics, 3rd ed.
- Grimmett, G. and Stirzaker, D. (2020) Probability and Random Processes 3rd ed.
- Karlin, S and Taylor, H. W. (1968) A First Course in Stochastic Processes 2nd ed.
- Lawer, G. F. (2006) Introduction to Stochastic Processes. Chapman & Hall/CRC Probability series, 2nd ed.
فرایندهای تصادفی ۱
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیش نیاز: احتمال ۲
حل تمرین: حداقل 17 ساعت
از جدول:
سر فصل درس و ریزمواد:
- مقدمه و تعریف فرایند تصادفی و بیان کاربردهای آنها
- فرایند برنولی: تعداد موفقیتها، زمانهای موفقیت، فرایند حاصل جمع متغبرها
- فرایندهای پواسن: ویژگیهای فرایند، ارتباط با توزیع نمایی، زمانهای ورود، فرایند پواسن ترکیبی
- زنجیرهای مارکف: توزیع اولیه، زمانهای اصابت، ماتریس انتقالات، وضعیتهای گذرا و بازگشتی، احتمالات جذب، زنجیرهای شاخه ای و صف بندی، تجزیه فضای مکان، مسأله بازیکن
- توزیعهای ایستا: خواص توزیعهای ایستا، زنجیر زاد و مرگ، زنجیرهای ساده نشدنی، وضعیتهای بازگشتی مثبت و پوچ، متوسط تعداد دفعات ملاقات از یک وضعیت بازگشتی، اشاره ای به روش مونت کارلو
- فرایندهای مارکف زمان پیوسته: فرایند جهشی محض، کاربردهای فرایند جهشی محض در فرایند زاد و مرگ و صف بندی
مراجع:
- Karlin, S. Taylor, H. M., A First Course in Stochastic Processes, 2th Ed., 1975
- Pierre, B., Markov Chains, Gibbs fields, Monte Carlo Simulation and Queues, Springer, New York, 1999
- Cinlar, E., Introduction to Stochastic Processes, 1975
- Karlin, S. Taylor, H. M., An Introduction to Stochastic Modeling, Academic Press, 4th Ed., 2011
- Ross, S. M., Stochastic Processes, 2th Ed. , 1996.
كنترل كيفيت آماری
تعداد واحد/ساعت: ۳ واحد/ ۵۱ ساعت
پیشنیاز: روشهای نمونهگیری ۲
حل تمرین: حداقل ۲۵ ساعت
از جدول: 3
سرفصلدرسوريزمواد :
- بهبودكيفيت:پيشينه وتكاملكنترلكيفيت، تعریف بهبود کیفیت، رابطه بین بهبود کیفیت و بهره وری، هزینه های کیفیت، روش های بهبود کیفیت ، نظامهايكيفيت،نظاممديريتكيفيتايزو 9000 ،مديريت كيفيتجامع
- روش های آماری در بهبود کیفیت : مدلسازی کیفیت فرآیند، استنباط درباره کیفیت فرآیند (یادآوری توزیع های آماری و استنباط آماری)
- كنترلآماريفرآيند: روش ها ی کنترل فرآیند آماری، مقدمهايبرنمودارهايكيفيت، نمودارهايكنترلبرايمتغيرهاي كيفي(وصفي)،نمودارهايكنترلبرايمتغيرهايكمي(متغير)،نمودارهايويژهكنترل،حدودمشخصاتطراحي(فني)و حدودرواداري، کنترل فرآیند آماری برای تولیدات کوتاه مدت ، تجزیه و تحلیل کارآیی فرآیند
- روشهايبهبودكيفيت : فنونكنترلفرآيندوبهبود،آزمايشهايصنعتي،طرحاستوار،قابليتاعتماد
- بازرسينمونهاي: بازرسينمونهايبرايمتغيرهايكيفي )وصفي)،بازرسينمونهايبرايمتغيرهايكمي(متغير)، روشهايويژهينمونهگيريهايمتغيرهايكيفي
مراجع:
- H. M. Wadsworth, K. S. Stephens, and A. B. Godfrey, Modern Methods for Quality Control and Improvement, 2nd Ed., 2000.
- D. C. Montgomery, Statistical Quality Control, John Wiley & Sons, 2009.
- مونتگومری، داگلاس سی، کنترل کیفیت آماری، ترجمه رسول نورالسناء، ویرایش سوم، چاپ دوازدهم، 1389، انتشارات دانشگاه علم و صنعت ایران.
مبانی ریاضی
ضرورت ارائهی درس:
یکی اهداف اصلی در اولین درسهای ریاضی آشنا شدن دانشجو با نحوه تفکر ریاضی و ارائه اثبات است. در این درس ضمن دنبال کردن این هدف، دانشجو با دو مفهوم بسیار اصلی در ریاضیات، یعنی مفهوم مجموعه و تابع نیز آشنا میشود. در عین حال مفاهیمی چون شمارشپذیری و ناشمارایی، کاردینالها و لم زورن نیز مورد بررسی قرار میگیرد. در ارتباط با هدف اولیه درس، یعنی آشنایی دانشجو با نحوه استدلال ریاضی، اصول اولیهای که ریاضیات بر پایه آنها بنا شده است بیان شده، عاری بودن یا نبودن ریاضیات از تناقض مورد بررسی قرار میگیرد.
شرح درس:
آشنایی با منطق گزارهها و منطق محمولها، منطق مرتبه اول، نظریه اصل موضوعی مجموعهها و بیان ضرورت آن با پرداختن به برخی تناقضها از جمله تناقض راسل، جبر بولی مجموعهها، خانواده اندیسدار مجموعهها، اجتماع و اشتراک یک خانواده، حاصلضرب دکارتی دو مجموعه، رابطه، رابطههای همارزی و ارتباط آنها با افرازها، مجموعه کلاسهای همارزی، ترکیب دو رابطه، تابع، تحدید و توسیع توابع، تابع یک به یک و پوشا، توابع وارون چپ و وارون راست، تابع وارون، همتوانی، مجموعههای متناهی و نامتناهی، مجموعههای شمارشپذیر و ناشمارا، شمارشپذیری مجموعه اعداد گویا و ناشمارایی مجموعه اعداد حقیقی، اعداد اصلی، ترتیب در اعداد اصلی، قضیه شرودر-برانشتاین، حساب اعداد اصلی مانند جمع و ضرب، توان اعداد اصلی، لم زورن، اصل خوشترتیبی، اصل انتخاب، ساختار اعداد.
محاسبات آماری با کامپیوتر
تعداد واحد/ساعت: ۳ واحد
پیش نیاز: رگرسیون ۱
حل تمرین: حداقل ۱۷
از جدول:
سرفصل درس و ریز مواد:
- معرفی نرم افزار و قابلیتهای آن، آشنایی با منوهای نرم افزار، نحوه گزارش خطاها، آشنایی با help نرم افزار.
- خواندن اطلاعات مجموعه دادهها به فرمتهای مختلف در این نرمافزار و قابلیت تلفیق چند مجموعه داده و انجام تغییرات در متغیرها و مشاهدات. ذخیره کردن دادههای موجود در نرم افزار به فرمتهای مختلف.
- استفاده از حلقهها و گزارههای شرطی و انجام عملیات جبری.
- محاسبه توابع چگالی، توابع توزیع و چندکهای توزیع.
- شبیهسازی از توزیعهای آماری معروف.
- مباحث مرتبط با رسم انواع نمودارهای آماری و تغییر مشخصات گرافیکی آنها.
- آزمون نرمال بودن توزیع و انجام آزمونهای نیکویی برازش جهت تشخیص انواع توزیعهای آماری.
- مباحث مرتبط با انواع آزمون فرضهای یک جامعه، دو جامعه و k جامعه، به صورت پارامتری و ناپارامتری.
- آزمون های استقلال و محاسبه انواع وابستگیها (پیرسون، اسپیرمن و ...)
- مباحث مرتبط با رگرسیون خطی ساده و رگرسیون چندگانه (برازش مدلها، مباحث مرتبط با همخطی چندگانه، انواع آزمون فرضهای مرتبط با ضرایب رگرسیونی، مقایسه مدلهای رگرسیونی در دو جامعه)
- بررسی فرضیات مدلهای رگرسیونی نظیر نرمال بودن ماندهها، ثبات واریانس و .. و راه حلهای مواجه با آن نظیر انجام تبدیلات باکس و کاکس و یا رگرسیون وزنی.
- تشخیص داده های دورافتاده، اهرم گون و تاثیرگذار در برازش مدلهای رگرسیونی.
- آنالیز واریانس یک راه و دو راهه، آنالیز کوواریانس.
- توانایی الگوریتمنویسی و نوشتن برنامهها.
- حل معادلات و انتگرالها.
ملاحظات:
قسمت اعظم ارزشیابی درس منوط به انجام تکالیف گروهی و انفرادی با تاکید بر تشخیص مساله و انجام تفسیرهای صحیح است.
ترجیحا مجموعه دادههای واقعی با تعداد مشاهدات و متغیرهای زیاد در اختیار دانشجویان قرار داده شود.
نرم افزارهای آماری با قابلیت برنامه نویسی در این درس تدریس میشوند نظیر: SAS، R، SPLUS و STATA.
مراجع:
متناظر با نرم افزار مورد تدریس تعیین میگردد.
منطق ریاضی
ضرورت ارائهی درس
درس منطق ریاضی، اهمیتی فراتر از یک درس در دانشکدهی ریاضی دارد. در این درس، قضایایی بیان و اثبات میشوند که نه تنها در تقویت پایهی ریاضی دانشجویان نقش دارند، بلکه در نگاه فلسفی آنها به علم و زندگی نیز تأثیرگذارند. مهمترین این قضایا، قضایای تمامیت و ناتمامیت گودل هستند که اهمیت آنها ریاضیات قرن بیستم را تحت تأثیر خود قرار داده است. این قضایا نه تنها بر سیستمهای فکری ریاضی، بلکه بر تمامی سیستمهای تفکر بشری قابل اعمال هستند و درکشان در هیچ واحد درسی، غیر از منطق ریاضی امکانپذیر نیست. در راستای آشنا شدن با قضایای ذکر شده، دانشجو در درس منطق ریاضی فرصتی مییابد تا آشنائی عمیقتری با مبانی اصول موضوعهای ریاضی پیدا کند و محدودیتها و مزایای آنها را بشناسد. در واقع هر آنچه در درس مبانی ریاضی، به صورت گذرا و غیر دقیق به دانشجو تدریس میشود، در درس منطق ریاضی به صورت عمیقتر به او انتقال مییابد. دانشجو همچنین در این درس با مفاهیمی مانند درستی، اثباتپذیری و استنتاج، به همراه مفاهیمی مانند تصمیمپذیری و الگوریتم به دقیقترین صورت آشنا میشود. نیز در بخشهائی از این درس دانشجو با برخی تکنیکهای منطقی آشنا خواهد شد که او را در فهم سایر دروس دانشکده مانند جبر و آنالیز تواناتر میکنند.
شرح درس:
مروری بر منطق گزارهها، اثباتی از قضیهی فشردگی درمنطق گزارهها به صورت منطقی یا توپولوژیک، منطق مرتبهی اول، ساختارهای مرتبهی اول و همومرفیسمها، درستی و استنتاج، دستگاههای مختلف استنتاجی مانند دستگاه هیلبرت و دستگاه حساب رشتهای، قضیهی درونیابی، قضیهی درستی و تمامیت گودل، نظریهی مدل مقدماتی شامل قضایای فشردگی، لونهایم ــ اسکولم، حذف سور، آنالیز نااستاندارد، اثبات قضیهی فشردگی با استفاده از فرافیلترها، نتایج ریاضیاتی قضیهی فشردگی، محاسبهپذیری و بازگشتی بودن، تز چرچ ـ تورینگ، قضیهی ناتمامیت گودل در حساب یا در نظریهی مجموعهها، مبانی نظریهی پیچیدگی و مسألهی پی در برابر انپی.
نظریه گالوا
ضرورت ارائهی درس
قضیهی اساسی گالوا یکی از مهمترین قضایای جبری است که در درس نظریهی گالوا بیان و اثبات میشود. این قضیه پل ارتباطی میان نظریهی گروهها و نظریهی میدانها است. با توجه به این گفته، اهمیت این درس برای دانشجو از چندین منظر است: نخست دانشجو فرصتی مییابد تا دانش جبری خود، در نظریهی گروهها و در نظریهی میدانها را بسط دهد و آنچه در درس مبانی جبر فرا گرفته است مروری کاربردی کند. دوم، دانشجو با برخی مسائل کلاسیک ریاضیات در ارتباط با امکان ترسیم توسط خطکش و پرگار و رویکرد جبری بدین مسائل آشنا خواهد شد. سوم، در این درس دانشجو اثبات قضیهی اساسی جبر (یعنی قضیهای که بیانگر این است که همهی چندجملهایها در میدان اعداد مختلط ریشه دارند) را فرا خواهد گرفت. آشنائی با نظریهی گالوا در تقویت پایهی جبری دانشجویان و سوق دادن به سمت موضوعات جبری در تحصیلات تکمیلی نقش موثری خواهد داشت.
شرح درس:
مرور قضایای سیلو در نظریهی گروهها، حلقهها، زیرحلقهها، ایدهآلها، همومرفیسمها، میدانهای خارجقسمتی و حوزههای صحیح، مشخصهی میدان، حوزههای اقلیدسی و تجریهی یکتا، چندجملهایهای تحویلناپذیر، توسیعهای میدانها، درجهی توسیع، ترسیمهای توسط خطکش و پرگار، میدانهای متناهی، گروههای گالوا، اتومرفیسمهای میدانی و گروههای اتومرفیسمها، توسیع نرمال، توسیع جداشدنی، قضیهی اساسی نظریهی گالوا، اثبات قضیهی اساسی جبر با استفاده از نظریهی گالوا، درجهی و پایهی تعالی، حدس شانوئل، اثبات متعالی بودن برخی اعداد گنگ، گروههای بازگشتی، گروههای حلشدنی.
نظریه مقدماتی معادلات دیفرانسیل
ضرورت ارائهی درس
بسیاری از پدیدههای غیرخطی که در طبیعت و دنیای واقعی اتفاق میافتند توسط معادلات دیفرانسیل غیرخطی مدل میشوند. برای بررسی کیفی این پدیدهها لازم است که یک تحلیل ریاضی از معادلات دیفرانسیل غیرخطی انجام شود. این تحلیل با تعیین هندسه جریان یک معادله دیفرانسیل (یا همان نمای فاز) کامل میشود. بسیاری از مسائل کاربردی در فیزیک، شیمی، برق، مکانیک، زیست شناسی و پزشکی به چنین تحلیلی نیاز دارند. از آنجایی که معادلات دیفرانسیل غیرخطی را نمیتوان در حالت کلی به صورت تحلیلی حل کرد، لذا مطالعهی رفتار کیفی و مجانبی جوابها در کاربردها اهمیت پیدا میکند. هدف اصلی در این درس درک و فهم یا تعیین هندسهی منحنیهای جواب یک معادله دیفرانسیل در فضای فاز آن میباشد. این درس ابزاری را در اختیار ما قرار میدهد تا بتوانیم مقدار زیادی اطلاعات کیفی در مورد رفتار موضعی و سراسری جوابها بدست آوریم. این درس مفاهیم و ابزارهای اساسی را برای مطالعه نظریه سیستمهای دینامیکی در اختیار دانشجویان قرار میدهد. در این درس، دانشجویان با مبانی نظریه کیفی معادلات دیفرانسیل عادی و کاربردهای آن آشنا میشوند و یک درک هندسی از موضوع نصیب آنها میشود.
شرح درس:
معادلات اسکالر و نمای فاز آنها، نقاط تعادل و پایداری آنها، مجموعههای حدی، دیاگرام انشعاب معادلات اسکالر وابسته به پارامتر، نگاشت پوانکاره معادلات اسکالر و مشتقات آن، دستگاههای خطی در صفحه و دسته بندی نمای فاز آنها، قضیه اساسی برای دستگاههای خطی، قطری سازی، محاسبه ماتریس e^At برحسب مقادیر ویژه و بردارهای ویژه ماتریس مربعی A، فرمهای جردن، نظریه پایداری، زیر فضاهای خطی پایدار، ناپایدار و مرکزی یک دستگاه خطی، دستگاههای خطی غیر همگن، ماتریس اساسی جوابها و فرمول تغییر ثابت، قضیه لیوویل و کاربردهای آن، دستگاههای غیرخطی و نظریه موضعی، بازه ماگزیمال وجود جواب، جریان تعریف شده توسط یک معادله دیفرانسیل، خطی سازی، قضیه منیفلد پایدار، قضیه هارتمن-گروبمن، قضیه اساسی وجود و یکتایی، انتگرال اول و دستگاههای حافظ انرژی، دستگاههای نیوتنی، دستگاههای گرادیانی و همیلتونی، پایداری و توابع لیاپانوف، تحلیل صفحه فاز با استفاده از نگاشت پوانکاره.
نظریهی اعداد
ضرورت ارائهی درس:
محور اصلی درس نظریه اعداد مطالعه اعداد است. از شاخه های اصلی نظریه اعداد میتوان به نظریه جبری اعداد، نظریه تحلیلی اعداد، نظریه محاسباتی اعداد، نظریه احتمالاتی اعداد و نظریه ترکیبیاتی اعداد اشاره کرد. الگوریتم های اعداد اول وتوابع توزیع آنها به ویژه الگوریتمهای سریع برای امتحان اعداد اول و تجزیه اعداد صحیح در رمزنگاری و علوم کامپیوتر کاربردهای مهمی دارند.
هدف اصلی در این درس آشنایی با مفاهیم مقدماتی در مورد اعداد صحیح، اعداد اول، معادله های همنهشتی و معادله های سیاله است. ارائه این درس به عنوان درس اصلی در دوره کارشناسی ریاضی ضروری است.
شرح درس:
بخشپذیری، الگوریتم تقسیم، بزرگترین مقسوم علیه مشترک، الگوریتمهای سریع برای محاسبه بزرگترین مقسوم علیه مشترک، معادله های دیوفانتین خطی، اعداد اول، تجزیه به توانهای اعداد اول، توزیع اعداد اول، اعداد اول فرما و مرسن، هم نهشتیها، محاسبات پیمانه ای، هم نهشتیهای خطی، قضیه باقیمانده چینی، حساب در Zp، قضیه کوچک فرما، تابع اویلر، اعداد شبه اول، هم نهشتیها در پیمانه توان یک عدد اول، گروه یکهها، ریشههای اولیه، ماندههای مربعی، نماد لژاندر، محک اویلر، لم گاوس، قانون تقابل مربعی، اعداد تام، توابع حسابی، حلقه توابع حسابی، دستور عکس موبیوس، مجموع مربعها، قضیه مجموع دو مربع، کسرهای مسلسل، حل برخی معادلههای دیوفانتین، کاربرد فراگیر اعداد اول در رمزنگاری، آشنایی با نرم افزارهای ریاضی برای پیاده سازی الگوریتمهای ارائه شده در این درس.
نظریهی مجموعهها
اهمیت و ضرورت ارائهی درس
اصول موضوعهی علم ریاضی نوین بر پایهی نظریهی مجموعهها بنا شده است. از این رو آشنائی با نظریهی مجموعهها برای دانشجویان دغدغهمند ریاضی، اجتنابناپذیر است.
درس نظریهی مجموعهها، به عنوان درسی تخصصی در گرایش منطق ریاضی، در ادامهی درس مبانی ریاضی قرار میگیرد. هر آنچه در درس مبانی ریاضی به صورت گذرا و احتمالاً نادقیق بیان شده است در این درس به صورت پایهای بیان و اثبات میشود.
همچنین در این درس به سوالات بنیادین علم ریاضی، مانند وجود مجموعهها، سازگاری نظریهی مجموعهها و در پی آن سازگاری علم ریاضی و استقلال برخی قضایا از اصول نظریهی مجموعهها پرداخته میشود. در این درس مجموعههای اعداد بازشناسانده میشود و کاردینالها و اردینالهای نامتناهی مختلف مورد مطالعه قرار میگیرند. همچنین با استفاده از تکنیک فُرسینگ، به ساختن مدلهائي از ریاضیات پرداخته میشود که در آنها پدیدههائي مانند حدس پیوستار برقرار باشند.
آشنائی با این درس موجب گسترده شدن افق دید دانشجو نسبت به مسائل بنیادین و فلسفی ریاضی میشود.
شرح درس
اصول برنیز ـ گودل برای کلاسها و اصول زرملو ـ فرانکل برای مجموعهها، اصل خوشترتیبی، اصل انتخاب، لم زرن، اردینالها و حساب آنها، قضایای بازگشت، استقرای فرامتناهی، اعداد طبیعی و سلسلهمراتبِ فوننویمن، کاردینالها و توانهای آنها، همپایانی و کاردینالهای منظم، کلابها و مجموعههای ساکن، قضایای رمزی و اردوشرادو، قضیهی سیلور، قضیهی کونیگ، کاردینالهای فشردهی ضعیف، کاردینالهای اندازهپذیر، مدلهای متعدی نظریهی مجموعهها، برابریِ V=L، فرسینگ و مدلهای ژنریک، سازگاری نظریهی مجموعهها
منابع درس
- Kunnen, K. (2011). Set theory (revised). London: college publication.
- Jech, T. (2013). Set theory (2, illustrated). Newyork: Springer science and business media.
- Levy, A. (1979), Basic set theory, Berlin: Springer
- Enderton, H (1977), Elements of set theory, Academic Press
- Ebbinghaus (2003), Einfuhrung in die Mengenlehre (4), Mannheim: Hochschultaschenbuch
- Halbeisen L.(2012), Combinatorial set theory, Berlin: Springer
- Kanamori A (2009), The higher infinite (2), Berlin: Springer-Verlag
Ziegler, M (2010), Mathematische Logik, Basel: Birkhäuser, Mathematik kompakt
هندسه جبری مقدماتی
ضرورت ارائهی درس
درس هندسه جبری یکی زیباترین و فعالترین شاخههای ریاضی محسوب میشود که با توجه به طبیعت بین رشتهای آن امکان درک بهتر مفاهیم جبری و هندسی را فرآهم میکند. از طرفی با توجه به اینکه این درس مبتنی بر روشهای محاسباتی ارائه میشود به درک بهتر دانشجویان از مفاهیمی مانند الگوریتم و پیچیدگی محاسباتی کمک میکند.
شرح درس:
یادآوری مفاهیمی مانند گروه، حلقه، میدان و ایدهآل، ساختار میدانهای متناهی، حلقه چندجملهای های تکمتغیره، الگوریتم تقسیم، الگوریتم محاسبه ب.م.م.، حلقه چندجملهایهای چندمتغیره، حلقه خارجقسمتی، ایدهآل تکجملهای، لم دیکسون، ترتیب تکجملهای، الگوریتم تقسیم در حلقه چندجملهایهای چندمتغیره، پایه گربنر، قضیه پایهای هیلبرت، خواص پایه گربنر، محک بوخبرگر، الگوریتم بوخبرگر، چندگونای آفین، ایدهآل یک چندگونا، ایدهآل حذفی، نظریه حذف، حل دستگاه معادلات چندجملهای، قضیههای ضعیف و قوی صفرسازهای هیلبرت، قضیه مکالی، بعد ایدهآل، توپولوژی زاریسکی، قضیه بستار، کاربردهای پایه گربنر در صریحسازی، قضیه تابع معکوس، نظریه اعداد و برنامهریزی خطی
هندسه دیفرانسیل
ضروت ارائهی درس
هندسه دیفرانسیل بعنوان شاخهای از ریاضیات با هدف مطالعهُ خواص هندسی با استفاده از ابزار حساب دیفرانسیل و انتگرال، نه فقط برای ایجاد دیدگاه جدیدی از جهان پیرامون برای دانشجو اهمیت دارد، بلکه مقدمهای برای درک مطالب پیشرفتهتر دروس کارشناسی و مقاطع بالاتر است. این درس تقریباً در همهُ دانشگاههای طراز اول دنیا از دروس اصلی دانشکدههای ریاضی و حتی فیزیک است. برای بیان اهمیت این درس برای دانشجویان ریاضی و غیر ریاضی، در ادامه به علوم دیگری که با مباحث هندسه دیفرانسیل سرو کار دارند و برخی کاربردهای آن در این علوم اشاره میکنیم: فیزیک (نظریه نسبیت عام اینشتین، الکترومغناتیس، مکانیکهای لاگرانژ و هامیلتون، ترمودینامیک)، شیمی و بیوفیزیک (مدلسازی غشاء سلولی تحت فشار متغیر)، اقتصاد (اقتصاد متری)، مدلسازی هندسی (طراحی هندسی به کمک کامپیوتر و گرافهای کامپیوتری)، نظریه کنترل (آنالیز کنترلکنندههای غیر خطی)، آمار، احتمال و نظریه اطلاعات (هندسه اطلاعات)، زمینشناسی (آنالیز و توصیف ساختارهای ژئودزیک).
شرح درس:
خمهای پارامتری، پارامتری سازی مجدد، انحنا، خمهای مسطح، خمهای فضایی، انحناِی خمهای فضایی، تاب و کنج فرنه، معادلات طبیعی، حرکات صلب، قضیههای هاف و جردن، قضیه گرین. رویهها، رویههای پارامتری، رویههای عادی(منظم) و صفحه مماس، تغییر مختصات، رویههای جهتپذیر، مساحت رویه، اولین و دومین فرم اساسی، اولین و دومین فرم اساسی در مختصات موضعی. انحنای یک رویه، نگاشت گاوس، انحناهای قائم و اصلی، انحناهای گاوسی و متوسط، مختصات موضعی، رویههای خطکشی شده و رویههای کمینه، معادلات اساسی رویهها، نمادگذاری تانسوری، معادله گاوس و نمادهای کریستوفل، معادلات کٌدازی و قضیه شگفتانگیز، قضیه اساسی نظریه رویهها. خمها روی رویهها، انحناها و تاب، مختصات ژئودزی، قضیه گاوس-بونه و کاربردها، هندسه ذاتی.
برنامه درسی ورودیهای ۹۷ به قبل
تا پیش از ورودیهای ۹۸، درسها عموماً سهواحدی بودند. درسهای دانشکده برای دانشجویان ورودی ۹۷ به قبل، مطابق زیر است.
دروس دوره کارشناسی آمار و کاربردها
دروس دوره کارشناسی ریاضیات و کاربردها
این درسها مطابق جداول زمانبندی زیر به دانشجویان ارائه میشوند:
برنامه زمانبندی کارشناسی آمار و کاربردها
برنامه زمانبندی کارشناسی ریاضیات و کاربردها
همچنین در نمودارهای زیر، چگونگی پیشنیازی و همنیازی درسها مشخص شده است:
برنامهی پیشنهادی برای دانشجویان رشتهی آمار ورودی ۹۸ به بعد
همچنین برنامهی درسی پیشنهادی دانشکده، برای دانشجویان رشتهی آمار به صورت زیر است:

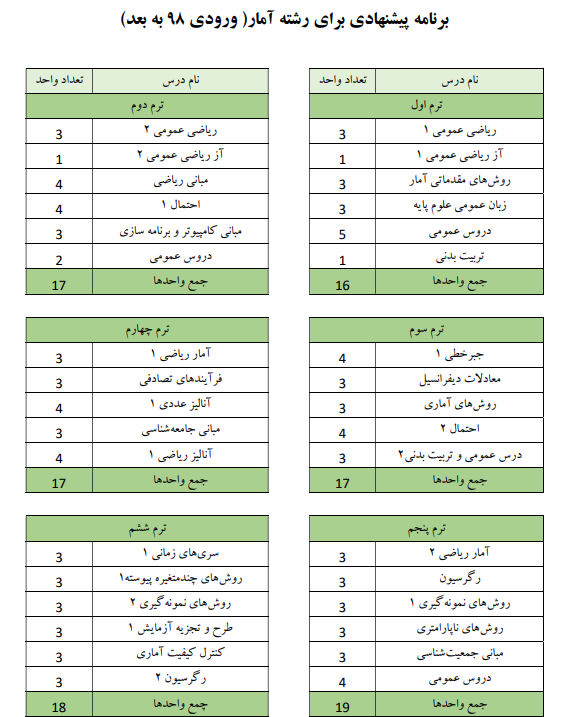
در این پیوند جداول مربوط به گروه آمار قرار داده شده است.
برنامهی پیشنهادی برای دانشجویان رشتهی ریاضیات و کاربردها ورودی ۹۸ به بعد
برنامهریزی پیشنهادی دانشکده برای دانشجویان ورودی ۹۸ در رشتهی ریاضیات و کاربردها به بعد به صورت زیر است:

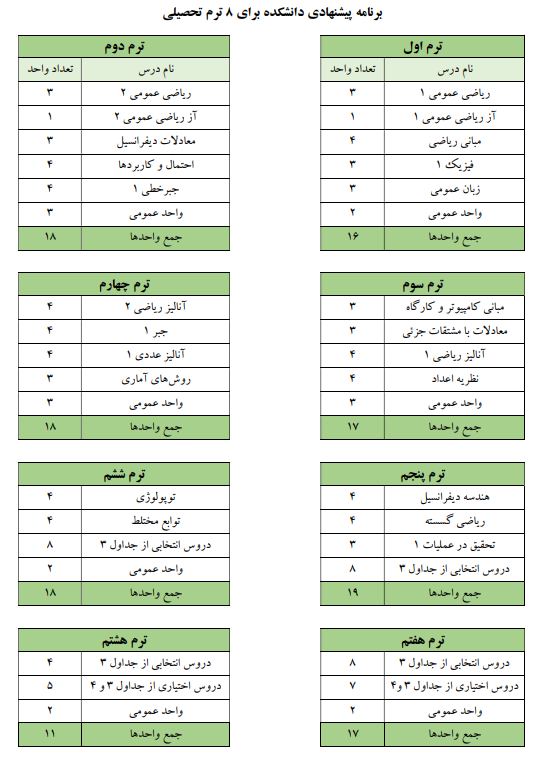
درسهائی که در جداول زیر آمدهاند، درسهای انتخابی نامیده میشوند. اخذ ۸ واحد از جدول زیر برای دانشجویان الزامی است:

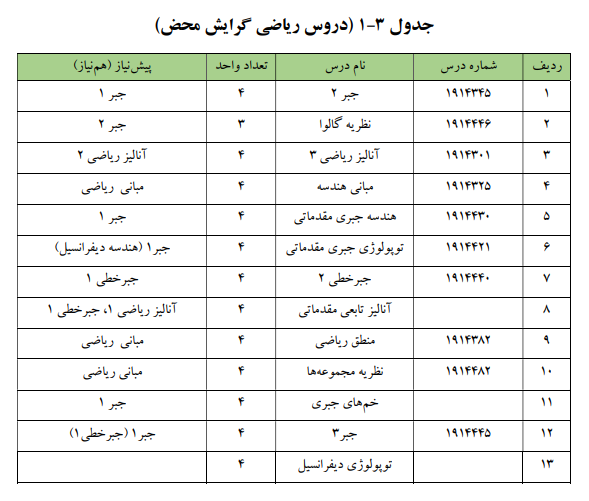
همچنین اخذ ۸ واحد از دروس جدول زیر نیز برای دانشجویان الزامی است:
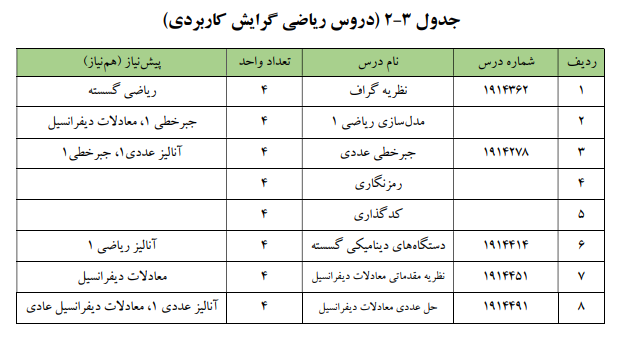
علاوه بر واحدهای انتخابی، برخی درسها به صورت «واحدهای اختیاری» ارائه شده اند. اخذ ۱۲ واحد از یکی از جداول ۳-۱ تا ۳-۸ در میان واحدهای اختیاری، الزامی است. علاوه بر آن دروس جدول ۴ نیز اختیاری هستند.

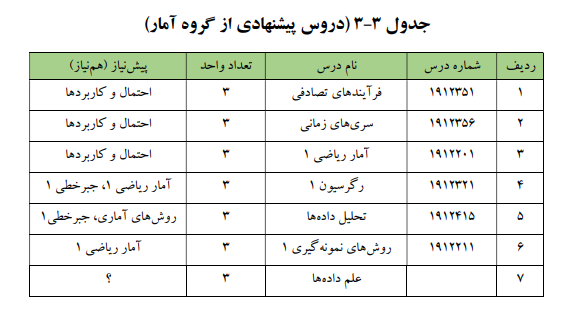

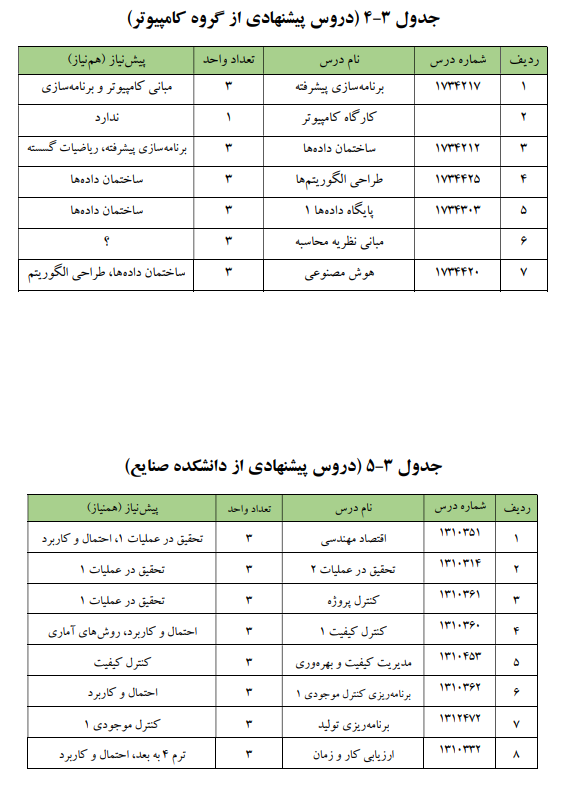


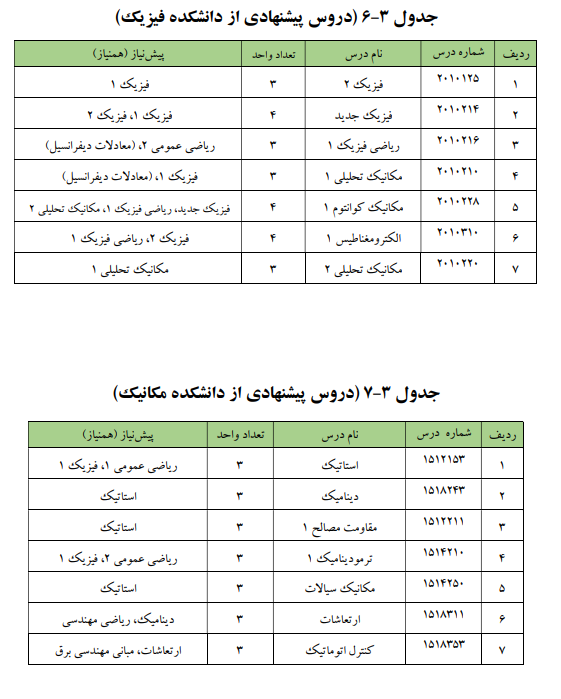
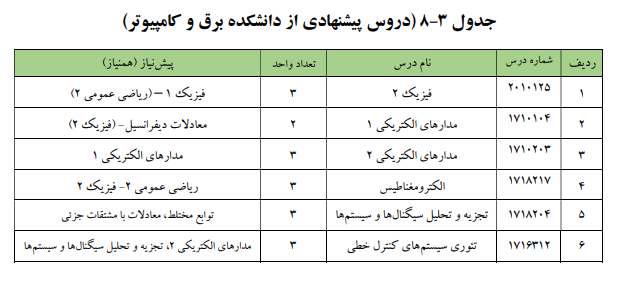
درسهای جدول زیر درسهای اختیاری نام دارند:
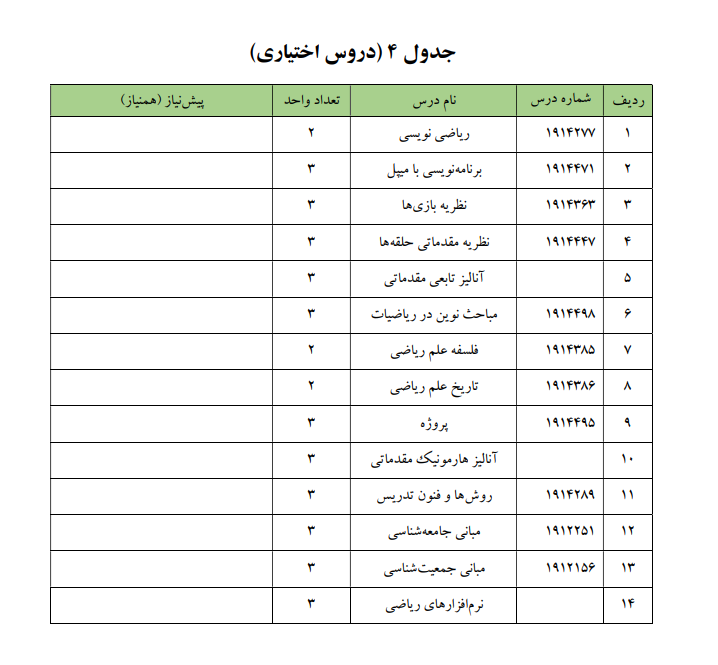
در این پیوند، جداول بالا به طور رسمیتر توضیح داده شدهاند.
برنامهی ویژهی دانشجویان دورشتهای ورودی ۹۸ به بعد


- 31-33913618 (98+)






