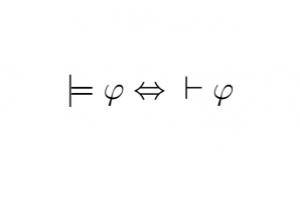منطق

در اواخر قرن نوزدهم ریاضیدانان به فکر ارائهٔ اصول موضوعه‌‌ٔ اصلی ریاضیات در هندسه، آنالیز و حساب افتادند، به طوری که بتوان بازگشت همهٔ قضایا به این اصول موضوعه را رصد کرد. در اوایل قرن بیستم، سوال معروف هیلبرت مطرح شد که آیا ممکن است که از اصول اولیه‌ای که برای ریاضیات در نظر گرفته شده است، تناقض نتیجه شود. نتایجی از گودل و گنتزن حکایت از آن داشت که برای اثبات عدم وجود تناقض در ریاضیات محدودیتهایی وجود دارد.  با این حال، پیشرفتهای نظریه‌ٔ مجموعه‌ها نشان داد که برای اصل‌بندی ریاضیات روزمره، نظریهٔ مجموعه‌ها چهارچوب مناسبی است؛ هر چند قضایائی باقی‌ می‌ماند که با استفاده از اصول نظریهٔ مجموعه‌ها نه اثبات و نه رد می‌شوند. موضوعات اینچنین، منجر به پیدایش و پیشرفت گرایش منطق ریاضی شد. درواقع تلاش برای درک و استحکام مبانی اصول‌موضوعه‌ای ریاضی، هدف گرایش منطق ریاضی است.

منطق ریاضی شامل چهار گرایش اصلی است: نظریهٔ مجموعه‌ها، نظریهٔ‌ مدلها، نظریه‌ٔ اثبات و نظریه‌ٔ بازگشت. در نظریه‌ٔ‌ اثبات به روشهای متناهی استنتاج قضایا بدون توجه به معانی آنها پرداخته می‌شود. در نظریه‌ی مدلها، به جهانهائی پرداخته می‌شود که قضایا در آنها برقرار هستند و  از این رو نظریه‌ٔ مدلها ارتباط تنگاتنگی با سایر شاخه‌های ریاضی مانند جبر و حساب دارد. قضیه‌ی مهم درستی و تمامیت گودل (تصویر مربوط به این بخش را ببینید) بیانگر این است که قضایای اثبات‌پذیر  دقیقاً آنهائی هستند که در همه‌ٔ جهانها درستند؛ و از این رو نظریهٔ مدلها و نظریه‌ی اثبات با هم در ارتباطند. نظریه‌ٔ بازگشت به نتایج قضایای مبانی ریاضیات در علوم رایانه می‌‌پردازد، از جمله به این که تا چه حد از ریاضیات قابل پیاده‌سازی توسط الگوریتم است.

در دانشکده‌ٔ‌ ریاضی افراد زیر در گرایش منطق فعالیت دارند. با کلیک روی نام هر یک می‌توانید با زمینهٔ‌ کاری و آثار آنها آشنا شوید. 
 

محسن خانی (نظریه‌ٔ مدلها)

مجتبی آقائی (منطق ریاضی، نظریه‌ی رمزی، فلسفه‌ علم ریاضیات، تاریخ علم ریاضیات)